分析:(1)由a
1=1,a
2=2,且a
2n-1,a
2n,a
2n+1成等差数列,a
2n,a
2n+1,a
2n+2成等比数列递推可得a
3=3,a
5=6,
a4=,a
6=8.
(2)由(1)猜想出通项公式,再用数学归纳法证明,要注意递推的严密性,
(3)由(1)求得
=,用数学归纳法证明
Sn<.
解答:解:(1)由已知,得a
3=3,a
5=6,
a4=,a
6=8.(2分)
(2)
a1==,
a3==,
a5==,;
a2=,
a4=,
a6=,.
∴猜想
a2n-1=,
a2n=,n∈N*,(4分)
以下用数学归纳法证明之.
①当n=1时,a
2×1-1=a
1=1,
a2×1==2,猜想成立;
②假设n=k(k≥1,k∈N*)时,猜想成立,即
a2k-1=,
a2k=,
那么
a2(k+1)-1=a2k+1=2a2k-a2k-1=2×-=,
a2(k+1)=a2k+2====.
∴n=k+1时,猜想也成立.
由①②,根据数学归纳法原理,对任意的n∈N*,猜想成立.(6分)
∴当n为奇数时,
an==;
当n为偶数时,
an==.
即数列{a
n}的通项公式为
an=.(9分)
(3)由(2),
得
=.
以下用数学归纳法证明
Sn<,n∈N*.
①当n=1时,
S1==1<=;
当n=2时,
S2=+=1+=<2=.
∴n=1,2时,不等式成立.(11分)
②假设n=k(k≥2)时,不等式成立,即
Sk<,
那么,当k为奇数时,
Sk+1=Sk+<+=
+4[+-]=-<;
当k为偶数时,
Sk+1=Sk+<+=
+4[+-]=-<.
∴n=k+1时,不等式也成立.
由①②,根据数学归纳法原理,对任意的n∈N*,不等式
Sn<成立.(14分)
点评:本题主要考查等差数列、等比数列、递推数列的有关概念,考查归纳推理、数学归纳法、分类讨论、不等式的放缩等重要数学思想方法,并对学生的创新意识、推理论证能力、运算求解能力进行了考查.



 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案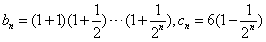 ,求证:对任意的n∈N*,
,求证:对任意的n∈N*,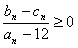 。
。 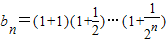 ,
,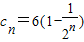 ,求证:对任意的n∈N*,
,求证:对任意的n∈N*,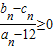 .
.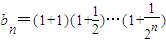 ,
,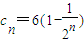 ,求证:对任意的n∈N*,
,求证:对任意的n∈N*,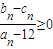 .
.