
【题目】如图,四棱锥P﹣ABCD的底面是矩形,PA⊥底面ABCD,PA=AD,点E、F分别为棱AB、PD的中点. (Ⅰ)求证:AF∥平面PCE;
(Ⅱ)AD与平面PCD所成的角的大小.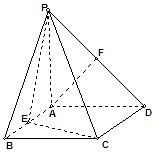
【答案】解:(Ⅰ)证明:取PC的中点G,连结FG、EG, 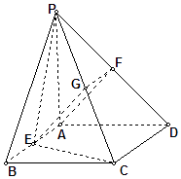
∴FG为△CDP的中位线,
∴FG ![]() CD,
CD,
∵四边形ABCD为矩形,E为AB的中点,
∴AE ![]() CD,
CD,
∴FG ![]() AE,
AE,
∴四边形AEGF是平行四边形,
∴AF∥EG又EG平面PCE,
AF平面PCE,
∴AF∥平面PCE;
(Ⅱ)∵PA⊥底面ABCD,
∴PA⊥AD,PA⊥CD,
又AD⊥CD,PA∩AD=A,
∴CD⊥平面ADP
又AF平面ADP,
∴CD⊥AF
在直角三角形PAD中,PA=AD且F是PD的中点,
∴AF⊥PD,
又CD∩PD=D,
∴AF⊥平面PCD.
∴∠ADP就是AD与平面PCD所成的角.
在直角三角形PAD中,PA=AD,
∴∠PDA=45°
∴AD与平面PCD所成的角是45°.
【解析】(Ⅰ)取PC的中点G,连结FG、EG,则FG ![]() CD,AE
CD,AE ![]() CD,因此FG
CD,因此FG ![]() AE,AF∥EG又EG平面PCE,AF平面PCE,AF∥平面PCE;(Ⅱ)PA⊥底面ABCD,可证明CD⊥平面ADP,CD⊥AF,则AF⊥PD,AF⊥平面PCD,∠ADP就是AD与平面PCD所成的角,PA=AD,∠PDA=45°.
AE,AF∥EG又EG平面PCE,AF平面PCE,AF∥平面PCE;(Ⅱ)PA⊥底面ABCD,可证明CD⊥平面ADP,CD⊥AF,则AF⊥PD,AF⊥平面PCD,∠ADP就是AD与平面PCD所成的角,PA=AD,∠PDA=45°.
【考点精析】掌握直线与平面平行的判定和空间角的异面直线所成的角是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则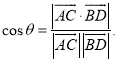 .
.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为 (为参数).在以坐标原点为极点,轴的正半轴为极轴的极坐标系中,曲线
(为参数).在以坐标原点为极点,轴的正半轴为极轴的极坐标系中,曲线![]() :
: ![]() .
.
(Ⅰ)求曲线![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若![]() 与
与![]() 相交于
相交于![]() 两点,设点
两点,设点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,且f(x)在(﹣∞,0]上单调递减,则不等式f(lgx)>f(﹣2)的解集是( )
A.( ![]() ,100)
,100)
B.(100,+∞)
C.( ![]() ,+∞)
,+∞)
D.(0, ![]() )∪(100,+∞)
)∪(100,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有若干(大于20)件某种自然生长的中药材,从中随机抽取20件,其重量都精确到克,规定每件中药材重量不小于15克为优质品.如图所示的程序框图表示统计20个样本中的优质品数,其中![]() 表示每件药材的重量,则图中①,②两处依次应该填的整数分别是____________.
表示每件药材的重量,则图中①,②两处依次应该填的整数分别是____________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为[﹣1,2],则函数g(x)=f(2x﹣ ![]() )的定义域为( )
)的定义域为( )
A.[ ![]() ,
, ![]() ]
]
B.[1, ![]() ]
]
C.[﹣1, ![]() ]
]
D.[﹣1, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某青少年成长关爱机构为了调研所在地区青少年的年龄与身高壮况,随机抽取6岁,9岁,12岁,15岁,18岁的青少年身高数据各1000个,根据各年龄段平均身高作出如图所示的散点图和回归直线![]() .根据图中数据,下列对该样本描述错误的是( )
.根据图中数据,下列对该样本描述错误的是( )
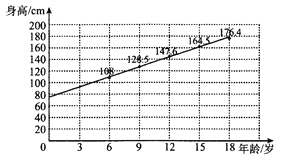
A. 据样本数据估计,该地区青少年身高与年龄成正相关
B. 所抽取数据中,5000名青少年平均身高约为![]()
C. 直线![]() 的斜率的值近似等于样本中青少年平均身高每年的增量
的斜率的值近似等于样本中青少年平均身高每年的增量
D. 从这5种年龄的青少年中各取一人的身高数据,由这5人的平均年龄和平均身高数据作出的点一定在直线![]() 上
上
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】集合A={(x,y)|y=a},集合B={(x,y)|y=bx+1,b>0,b≠1},若集合A∩B≠,则实数a的取值范围是( )
A.(﹣∞,1)
B.(﹣∞,1]
C.[1,+∞)
D.(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)= ![]() ,当点M(x,y)在y=f(x)的图象上运动时,点N(x﹣2,ny)在函数y=gn(x)的图象上运动(n∈N*).
,当点M(x,y)在y=f(x)的图象上运动时,点N(x﹣2,ny)在函数y=gn(x)的图象上运动(n∈N*).
(1)求y=gn(x)的表达式;
(2)若方程g1(x)=g2(x﹣2+a)有实根,求实数a的取值范围;
(3)设 ![]() ,函数F(x)=H1(x)+g1(x)(0<a≤x≤b)的值域为
,函数F(x)=H1(x)+g1(x)(0<a≤x≤b)的值域为 ![]() ,求实数a,b的值.
,求实数a,b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com