
【题目】(本题满分15分)某工厂某种航空产品的年固定成本为![]() 万元,每生产
万元,每生产![]() 件,需另投入成本为
件,需另投入成本为![]() ,当年产量不足
,当年产量不足![]() 件时,
件时,![]() (万元).当年产量不小于
(万元).当年产量不小于![]() 件时,
件时,![]() (万元).每件商品售价为
(万元).每件商品售价为![]() 万元.通过市场分析,该厂生产的商品能全部售完.
万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (件)的函数解析式;
(件)的函数解析式;
(2)年产量为多少件时,该厂在这一商品的生产中所获利润最大?
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:
【题目】(2015·湖南)某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖,求下列问题:(1)求顾客抽奖1次能获奖的概率(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为 X ,求 X 的分布列和数学期望.
(1)(1)求顾客抽奖1次能获奖的概率
(2)(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为![]() , 求
, 求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·江苏)如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1 , 设AB1的中点为D,B1CB![]() C1=E.求证:
C1=E.求证:
(1)DE∥平面AA1C1C
(2)BC1⊥AB1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (a>b>0)过点(0,
(a>b>0)过点(0,![]() ),且离心率为
),且离心率为![]() 。
。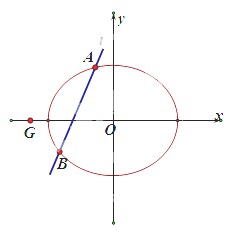
(Ⅰ)求椭圆E的方程;
(II)设直线x my 1,(m R)交椭圆E与A,B两点,判断点G(-![]() ,0)与以线段AB为直径的圆的位置关系,并说明理由。
,0)与以线段AB为直径的圆的位置关系,并说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖北)某厂用鲜牛奶在某台设备上生产![]() 两种奶制品.生产1吨A产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨B产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天B产品的产量不超过A产品产量的2倍,设备每天生产
两种奶制品.生产1吨A产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨B产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天B产品的产量不超过A产品产量的2倍,设备每天生产![]() 两种产品时间之和不超过12小时. 假定每天可获取的鲜牛奶数量W(单位:吨)是一个随机变量,其分布列为
两种产品时间之和不超过12小时. 假定每天可获取的鲜牛奶数量W(单位:吨)是一个随机变量,其分布列为
(Ⅰ)求Z的分布列和均值;该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利Z(单位:元)是一个随机变量.
(Ⅱ) 若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 对定义域内的每一个值
对定义域内的每一个值![]() 在其定义域内都存在唯一的
在其定义域内都存在唯一的![]() 使
使![]() 成立,则称该函数为“依赖函数”.
成立,则称该函数为“依赖函数”.
(1)判断函数![]() 是否为“依赖函数”,并说明理由;
是否为“依赖函数”,并说明理由;
(2)若函数![]() 在定义域
在定义域![]() 上为“依赖函数”,求实数
上为“依赖函数”,求实数![]() 乘积
乘积![]() 的取值范围;
的取值范围;
(3)已知函数![]() 在定义域
在定义域![]() 上为“依赖函数”,若存在实数
上为“依赖函数”,若存在实数![]() 使得对任意的
使得对任意的![]() 有不等式
有不等式![]() 都成立,求实数
都成立,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com