
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c,若a=5![]() sin(B
sin(B![]() ),c=5且O为△ABC的外心,G为△ABC的重心,则OG的最小值为( )
),c=5且O为△ABC的外心,G为△ABC的重心,则OG的最小值为( )
A.![]() 1B.
1B.![]() C.
C.![]() 1D.
1D.![]()
【答案】D
【解析】
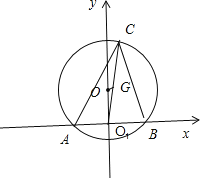
首先根据条件解△ABC可得:C![]() 和△ABC外接圆的半径R
和△ABC外接圆的半径R![]() ,由此建立直角坐标系,可得:.A(
,由此建立直角坐标系,可得:.A(![]() ,0),B(
,0),B(![]() ,0),外心O为(0,
,0),外心O为(0,![]() ),重心G
),重心G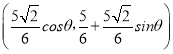 .从而求得|OG|2
.从而求得|OG|2![]() sinθ
sinθ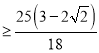 ,即可得解.
,即可得解.
A=5![]() sin(B
sin(B![]() ),c=5,
),c=5,
∴a![]() csin(B
csin(B![]() ),
),
由正弦定理可得:sinA![]() sinC
sinC![]()
![]() (sinB+cosB),
(sinB+cosB),
∴sin(B+C)=sinBcosC+cosBsinC=sinCsinB+sinCcosB,
化为:sinBcosC=sinC![]() sinB,sinB
sinB,sinB![]() 0,
0,
∴cosC=sinC,即tanC=1,C∈(0,π).
∴C![]() .
.
∴△ABC外接圆的半径R![]()
![]() .
.
如图所示,建立直角坐标系.A(![]() ,0),B(
,0),B(![]() ,0),O(0,
,0),O(0,![]() ).
).
△ABC外接圆的方程为:x2![]() .
.
设C(![]() cosθ,
cosθ,![]() sinθ).θ∈(0,π)
sinθ).θ∈(0,π)
则G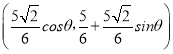 .
.
|OG|2![]() sinθ
sinθ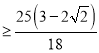 ,
,
∴|OG|的最小值为:![]() .
.
故选:D.


科目:高中数学 来源: 题型:
【题目】阿基米德是古希腊伟大的哲学家、数学家、物理学家,对几何学、力学等学科作出过卓越贡献.为调查中学生对这一伟大科学家的了解程度,某调查小组随机抽取了某市的100名高中生,请他们列举阿基米德的成就,把能列举阿基米德成就不少于3项的称为“比较了解”,少于三项的称为“不太了解”.
调查结果如下:
0项 | 1项 | 2项 | 3项 | 4项 | 5项 | 5项以上 | |
理科生(人) | 1 | 10 | 17 | 14 | 14 | 10 | 4 |
文科生(人) | 0 | 8 | 10 | 6 | 3 | 2 | 1 |
(1)完成如下![]() 列表,并判断是否由
列表,并判断是否由![]() 的把握认为.了解阿基米德与选择文理科有关?
的把握认为.了解阿基米德与选择文理科有关?
比较了解 | 不太了解 | 合计 | |
理科生 | p> | ||
文科生 | |||
合计 |
(2)在抽取的100名高中生中,按照文理科采用分层抽样的方法抽取10人的样本.
(i)求抽取的文科生和理科生的人数;
(ii)从10人的样本中随机抽取两人,求两人都是文科生的概率.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A、B两种品牌各三种车型2017年7月的销量环比(与2017年6月比较)增长率如下表:
A品牌车型 | A1 | A2 | A3 | ||||
环比增长率 | -7.29% | 10.47% | 14.70% | ||||
B品牌车型 | B1 | B2 | B3 | ||||
环比增长率 | -8.49% | -28.06% | 13.25% | ||||
根据此表中的数据,有如下关于7月份销量的四个结论:①A1车型销量比B1车型销量多;
②A品牌三种车型总销量环比增长率可能大于14.70%;
③B品牌三款车型总销量环比增长率可能为正;
④A品牌三种车型总销量环比增长率可能小于B品牌三种车型总销量环比增长率.
其中正确结论的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代劳动人民在筑城、筑堤、挖沟、挖渠、建仓、建囤等工程中,积累了丰富的经验,总结出了一套有关体积、容积计算的方法,这些方法以实际问题的形式被收入我国古代数学名著《九章算术》中.《九章算术》将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,如图所示的阳马三视图,则它的体积为( )
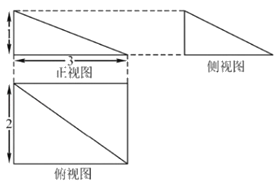
A.![]() B.1C.2D.3
B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3﹣(3a﹣2)x2﹣8x+12a+7,g(x)=lnx,记h(x)=min{f(x),g(x)},若h(x)至少有三个零点,则实数a的取值范围是( )
A.(﹣∞,![]() )B.(
)B.(![]() ,+∞)C.[
,+∞)C.[![]() ,
,![]() )D.[
)D.[![]() ,
,![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】冠状病毒是一个大型病毒家族,己知可引起感冒以及中东呼吸综合征(![]() )和严重急性呼吸综合征(
)和严重急性呼吸综合征(![]() )等较严重疾病.而今年出现在湖北武汉的新型冠状病毒(
)等较严重疾病.而今年出现在湖北武汉的新型冠状病毒(![]() )是以前从未在人体中发现的冠状病毒新毒株.人感染了新型冠状病毒后常见体征有呼吸道症状、发热、咳嗽、气促和呼吸困难等.在较严重病例中,感染可导致肺炎、严重急性呼吸综合征、肾衰竭,甚至死亡.
)是以前从未在人体中发现的冠状病毒新毒株.人感染了新型冠状病毒后常见体征有呼吸道症状、发热、咳嗽、气促和呼吸困难等.在较严重病例中,感染可导致肺炎、严重急性呼吸综合征、肾衰竭,甚至死亡.
某医院为筛查冠状病毒,需要检验血液是否为阳性,现有n(![]() )份血液样本,有以下两种检验方式:
)份血液样本,有以下两种检验方式:
方式一:逐份检验,则需要检验n次.
方式二:混合检验,将其中k(![]() 且
且![]() )份血液样本分别取样混合在一起检验.
)份血液样本分别取样混合在一起检验.
若检验结果为阴性,这k份的血液全为阴性,因而这k份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这k份血液究竟哪几份为阳性,就要对这k份再逐份检验,此时这k份血液的检验次数总共为![]() .
.
假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为p(![]() ).现取其中k(
).现取其中k(![]() 且
且![]() )份血液样本,记采用逐份检验方式,样本需要检验的总次数为
)份血液样本,记采用逐份检验方式,样本需要检验的总次数为![]() ,采用混合检验方式,样本需要检验的总次数为
,采用混合检验方式,样本需要检验的总次数为![]() .
.
(1)若![]() ,试求p关于k的函数关系式
,试求p关于k的函数关系式![]() ;
;
(2)若p与干扰素计量![]() 相关,其中
相关,其中![]() (
(![]() )是不同的正实数,
)是不同的正实数,
满足![]() 且
且![]() (
(![]() )都有
)都有![]() 成立.
成立.
(i)求证:数列![]() 等比数列;
等比数列;
(ii)当![]() 时,采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数的期望值更少,求k的最大值
时,采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数的期望值更少,求k的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,点
,点![]() 是矩形
是矩形![]() 内(含边界)的动点,且
内(含边界)的动点,且![]() ,
,![]() ,直线
,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .记点
.记点![]() 的轨迹长度为
的轨迹长度为![]() ,则
,则![]() ______;当三棱锥
______;当三棱锥![]() 的体积最小时,三棱锥
的体积最小时,三棱锥![]() 的外接球的表面积为______.
的外接球的表面积为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com