
分析 (1)求出函数f1(x)-f2((x)的单调性和最值,可得|f1(x)-f2(x)|∈[1,log26],由新定义即可判断;
(2)f1(x)与f2(x)在给定区间[a+2,a+3]上是接近的?|f1(x)-f2(x)|≤1?|loga(x-3a)-loga$\frac{1}{x-a}$|≤1?|loga[(x-3a)(x-a)]|≤1?a≤(x-2a)2-a2≤$\frac{1}{a}$对于任意x∈[a+2,a+3]恒成立.
解答 解:(1)当a=$\frac{1}{2}$时,函数f1(x)=$lo{g}_{\frac{1}{2}}$(x-$\frac{3}{2}$),f2(x)=$lo{g}_{\frac{1}{2}}$$\frac{1}{x-\frac{1}{2}}$,
f1(x)-f2(x)=$lo{g}_{\frac{1}{2}}$(x-$\frac{3}{2}$)-$lo{g}_{\frac{1}{2}}$$\frac{1}{x-\frac{1}{2}}$=$lo{g}_{\frac{1}{2}}$(x-$\frac{3}{2}$)(x-$\frac{1}{2}$)
=$lo{g}_{\frac{1}{2}}$[(x-1)2-$\frac{1}{4}$]在区间[$\frac{5}{2}$,$\frac{7}{2}$]上递减,
即有x=$\frac{5}{2}$时,取得最大值,且为-1,
x=$\frac{7}{2}$时,取得最小值,且为-log26,
则|f1(x)-f2(x)|∈[1,log26],
即有|f1(x)-f2(x)|>1.
则f1(x)与f2(x)在区间[a+2,a+3]上是非接近的;
(2)f1(x)与f2(x)在给定区间[a+2,a+3]上是接近的,
即为|f1(x)-f2(x)|≤1?|loga(x-a)-loga$\frac{1}{x-a}$|≤1
?|loga(x-3a)(x-a)|≤1
?a≤(x-2a)2-a2≤$\frac{1}{a}$对于任意x∈[a+2,a+3]恒成立.
设h(x)=(x-2a)2-a2,x∈[a+2,a+3],
且其对称轴x=2a<2在区间[a+2,a+3]的左边,
?$\left\{\begin{array}{l}{a≤h(x)_{min}}\\{\frac{1}{a}≥h(x)_{max}}\end{array}\right.$?$\left\{\begin{array}{l}{a≤h(a+2)}\\{\frac{1}{a}≥h(a+3)}\end{array}\right.$?$\left\{\begin{array}{l}{a≤4-4a}\\{\frac{1}{a}≥9-6a}\end{array}\right.$
?$\left\{\begin{array}{l}{a≤\frac{4}{5}}\\{a≤\frac{9-\sqrt{57}}{12}或a≥\frac{9+\sqrt{57}}{12}}\end{array}\right.$?0<a≤$\frac{9-\sqrt{57}}{12}$,
所以,当0<a≤$\frac{9-\sqrt{57}}{12}$,f1(x)与f2(x)在给定区间[a+2,a+3]上是接近的.
点评 本题考查新定义和对数函数的性质和应用,解题时要注意函数恒成立的充要条件的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -$\frac{1}{2}$ | C. | -1或-$\frac{1}{2}$ | D. | 1或-$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{9}$,+∞) | B. | (-∞,$\frac{1}{9}$] | C. | [$\frac{10}{9}$,+∞) | D. | (-∞,$\frac{10}{9}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A⊆B | B. | A∈B | C. | A与B无关系 | D. | A?B |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
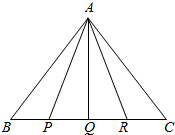 若P、Q、R是边长为1的正△ABC边BC上的四等分点,则$\overrightarrow{AB}$•$\overrightarrow{AP}$+$\overrightarrow{AP}$•$\overrightarrow{AQ}$+$\overrightarrow{AQ}$•$\overrightarrow{AR}$+$\overrightarrow{AR}$•$\overrightarrow{AC}$=$\frac{13}{4}$.
若P、Q、R是边长为1的正△ABC边BC上的四等分点,则$\overrightarrow{AB}$•$\overrightarrow{AP}$+$\overrightarrow{AP}$•$\overrightarrow{AQ}$+$\overrightarrow{AQ}$•$\overrightarrow{AR}$+$\overrightarrow{AR}$•$\overrightarrow{AC}$=$\frac{13}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com