
����Ŀ����һ��ͬѧ�ҿ���һ���̲�꣬��Ϊ���о����¶����̲����۱�����Ӱ�죬��һ���������ѡȡ5�죬ͳ�Ƴ����������̲����۱����������
���� | 0 | 4 | 12 | 19 | 27 |
���̲����۱��� | 150 | 132 | 130 | 104 | 94 |
���������̲����۱����������µ����Իع鷽��![]() ��
��![]() ��ȷ��0.1������ij�������Ϊ
��ȷ��0.1������ij�������Ϊ![]() ��Ԥ���������̲�����۱�����
��Ԥ���������̲�����۱�����
���ӱ��е�5������ȡ���죬����ѡȡ������������һ�����̲����۱�������130�ĸ��ʣ�
�ο����ݣ�![]() ��
��![]() .
.
�ο���ʽ�� ��
��![]() ��
��
���𰸡���1��![]() ��2.0x+146.8��Ԥ������Ϊ15oC�����̲�����Լ117������2��
��2.0x+146.8��Ԥ������Ϊ15oC�����̲�����Լ117������2��![]() ��
��
��������
��1���ɱ��������ݼ���![]() ��
��![]() ������ع�ϵ������д���ع鷽�̣�
������ع�ϵ������д���ع鷽�̣�
���ûع鷽����ö�Ӧ![]() ��ֵ��
��ֵ��
��2�������оٷ���������¼������ټ�������ĸ���ֵ��
��1���ɱ��������ݿɵã�
![]() =
=![]() ����0+4+12+19+27��=12.4��
����0+4+12+19+27��=12.4��![]() =
=![]() ����150+132+130+104+94��=122��
����150+132+130+104+94��=122��
��![]() =
= =
=![]() �֩�2.0��
�֩�2.0��
![]() =
=![]()
![]()
![]() =122������2.0����12.4=146.8��
=122������2.0����12.4=146.8��
�����̲����۱����������µ����Իع鷽��Ϊ
![]() =��2.0x+146.8��
=��2.0x+146.8��
��x=15ʱ��![]() =��2.0��15+146.8=116.8��117��
=��2.0��15+146.8=116.8��117��
��Ԥ������Ϊ15oC���������̲�����Լ117����
��2���DZ��еĵ�1�쵽��5��ΪA��B��c��d��e���������۱�������130����A��B��
��ȡ������AB��Ac��Ad��Ae��Bc��Bd��Be��cd��ce��de��10�������
����������һ�����۱�������130��AB��Ac��Ad��Ae��Bc��Be��7�������
����ѡȡ������������һ�����̲����۱�������130�ĸ���ΪP=![]() ��
��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ߵĶ�����ԭ��,����A(-4,4)�ҽ�����x��.
��1���������߷���;
��2��ֱ��l������B(-1,0)����������ཻ�����ҳ�Ϊ8,��ֱ��l�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABCD�У�PA��ƽ��ABCD��AB=BC=2����ABC=120�㣬AD=CD= ![]() ��ֱ��PC��ƽ��ABCD���ɽǵ�����Ϊ
��ֱ��PC��ƽ��ABCD���ɽǵ�����Ϊ ![]() ��
�� 
��1����EΪֱ��PC������һ�㣬��֤��AE��BD��
��2��������B��PC��A������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����P��˫���� ![]() ��
�� ![]() =1��a��0��b��0������֧�ϣ������ҽ���ֱ�ΪF1 �� F2 �� ֱ��PF1��������ԭ��OΪԲ�ġ�aΪ�뾶��Բ�����ڵ�A���߶�PF1�Ĵ�ֱƽ����ǡ�ù���F2 �� ���˫���ߵĽ����ߵ�б��Ϊ ��
=1��a��0��b��0������֧�ϣ������ҽ���ֱ�ΪF1 �� F2 �� ֱ��PF1��������ԭ��OΪԲ�ġ�aΪ�뾶��Բ�����ڵ�A���߶�PF1�Ĵ�ֱƽ����ǡ�ù���F2 �� ���˫���ߵĽ����ߵ�б��Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=ex+be��x��2asinx��a��b��R����
��1����a=0ʱ�����ۺ���f��x���ĵ������䣻
��2����b=��1ʱ����f��x����0������x�ʣ�0���У����������a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�У���A��B��C���Եı߷ֱ�Ϊa��b��c������ ![]() =��
=�� ![]() ��1����
��1���� ![]() =��cosA+1��sinA������
=��cosA+1��sinA������ ![]()
![]() ��ֵΪ2+
��ֵΪ2+ ![]() ��
��
��1�����A�Ĵ�С��
��2����a= ![]() ��cosB=
��cosB= ![]() �����ABC�������
�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʵ��x��y�����Լ������ 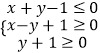 ����һ������Ͷ�����εõ��ĵ����ֱ�Ϊa��b������z=2ax+by�ڵ㣨2����1����ȡ�����ֵ�ĸ���Ϊ�� ��
����һ������Ͷ�����εõ��ĵ����ֱ�Ϊa��b������z=2ax+by�ڵ㣨2����1����ȡ�����ֵ�ĸ���Ϊ�� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() ��
��
��1������![]() �IJ���ʽ
�IJ���ʽ![]() ��һ��
��һ��![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2�������![]() �IJ���ʽ
�IJ���ʽ![]() ��
��
��3������![]() ������
������![]() ������㣬��ʵ��
������㣬��ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ�˻�����н�ͨѹ����������չ������ͨ���ᳫ���������ٿ�����Ϊ�˵�������˹������ĺ��������ͨ���ܲ��Ŵ���ijվ̨�ȳ���![]() ���˿��������ȡ
���˿��������ȡ![]() �ˣ��������ǵĺ�ʱ�䣨��λ�����ӣ���Ϊ�����ֳ�
�ˣ��������ǵĺ�ʱ�䣨��λ�����ӣ���Ϊ�����ֳ�![]() �飬���±���ʾ��
�飬���±���ʾ��
��� | һ | �� | �� | �� | �� | �� |
��ʱ�� |
|
|
|
|
|
|
���� |
|
|
|
|
|
|
��1��������![]() ���˿��к�ʱ������
���˿��к�ʱ������![]() ���ӵ�������
���ӵ�������
��2�������ϱ����ġ������![]() ���������ȡ
���������ȡ![]() ������һ�����ʾ����飬��鵽��
������һ�����ʾ����飬��鵽��![]() ��ǡ�����Բ�ͬ��ĸ��ʣ�
��ǡ�����Բ�ͬ��ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com