
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以平面直角坐标系的原点
为参数).以平面直角坐标系的原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求曲线![]() 和
和![]() 公共弦的长度.
公共弦的长度.
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:
【题目】设f(x)是R上的偶函数,且在[0,+∞)上单调递增,则f(-2),f(3),f(-![]() )的大小顺序是:( )
)的大小顺序是:( )
A. f(-![]() )>f(3)>f(-2) B. f(-
)>f(3)>f(-2) B. f(-![]() ) >f(-2)>f(3)
) >f(-2)>f(3)
C. f(-2)>f(3)> f(-![]() ) D. f(3)>f(-2)> f(-
) D. f(3)>f(-2)> f(-![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有偶数个球,其中红球、黑球各占一半,甲、乙、丙是三个空盒.每次从袋中任取两个球,将其中一个球放入甲盒,如果这个球是红球,就将另一个球放入乙盒,否则就放入丙盒.重复上述过程,直到袋中所有球都放入盒中,则( )
A. 乙盒中红球与丙盒中黑球一样多
B. 乙盒中黑球不多于丙盒中黑球
C. 乙盒中红球不多于丙盒中红球
D. 乙盒中黑球与丙盒中红球一样多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水泥厂销售工作人员根据以往该厂的销售情况,绘制了该厂日销售量的频率分布直方图,如图所示:
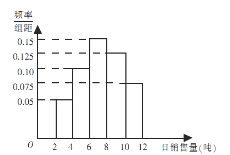
将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
(1)求未来3天内,连续2天日销售量不低于8吨,另一天日销售量低于8吨的概率;
(2)用![]() 表示未来3天内日销售量不低于8吨的天数,求随机变量
表示未来3天内日销售量不低于8吨的天数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以原点
中,以原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程并指出其形状;
的直角坐标方程并指出其形状;
(2)设![]() 是曲线
是曲线![]() 上的动点,求
上的动点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一盒中放有的黑球和白球,其中黑球4个,白球5个.
(1)从盒中同时摸出两个球,求两球颜色恰好相同的概率.
(2)从盒中摸出一个球,放回后再摸出一个球,求两球颜色恰好不同的概率.
(3)从盒中不放回的每次摸一球,若取到白球则停止摸球,求取到第三次时停止摸球的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象交于B、C两点,B(2,m)且m<2,正方形ABCD的顶点A、D在坐标轴上。
的图象交于B、C两点,B(2,m)且m<2,正方形ABCD的顶点A、D在坐标轴上。
⑴ 求![]() ,
, ![]() 的值;
的值;
⑵ 直接写出![]() 时,
时, ![]() 的取值范围。
的取值范围。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() (
(![]() )的图像关于坐标原点对称。
)的图像关于坐标原点对称。
(1)求![]() 的值,并求出函数
的值,并求出函数![]() 的零点;
的零点;
(2)若函数![]() 在
在![]() 内存在零点,求实数
内存在零点,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,若不等式
,若不等式![]() 在
在![]() 上恒成立,求满足条件的最小整数
上恒成立,求满足条件的最小整数![]() 的值。
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com