
【题目】已知奇函数 .
.
(1)求实数![]() 的值,并画出函数
的值,并画出函数![]() 的图象;
的图象;
(2)若函数![]() 在区间
在区间![]() 上是增函数,结合函数
上是增函数,结合函数![]() 的图象,求实数
的图象,求实数![]() 的取值范围;
的取值范围;
(3)结合图象,求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
【答案】(1) m=2. (2) (1,3].(3)最大值是1,最小值是-1.
【解析】
试题(1)根据奇函数定义得f(-x)=-f(x)代入可得m=2通过描点可得函数f(x)的图象;(2)根据图像可得[-1,a-2]为[-1,1]一个子集,结合数轴可得实数a满足的条件,解不等式可得a的取值范围(3)根据图像可得最高点与最低点,对应求出最大值和最小值.
试题解析:解:(1)当x<0时,-x>0,
则f(-x)=-(-x)2+2(-x)=-x2-2x.
又∵函数f(x)为奇函数,
∴f(-x)=-f(x).
∴f(x)=-f(-x)=-(-x2-2x)=x2+2x.
又∵当x<0时,f(x)=x2+mx,
∵对任意x<0,总有x2+2x=x2+mx,∴m=2.
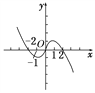
函数f(x)的图象如图所示.
(2)由(1)知f(x)=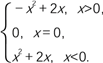
由图象可知,函数f(x)的图象在区间[-1,1]上的图象是“上升的”,
∴函数f(x)在区间[-1,1]上是增函数.
要使f(x)在[-1,a-2]上是增函数,
需有![]() 解得1<a≤3,
解得1<a≤3,
即实数a的取值范围是(1,3].
(3)由图象可知,函数f(x)的图象在区间[-2,2]上的最高点是(1,f(1)),最低点是(-1,f(-1)).
又因为f(1)=-1+2=1,f(-1)=1-2=-1,所以函数f(x)在区间[-2,2]上的最大值是1,最小值是-1.


科目:高中数学 来源: 题型:
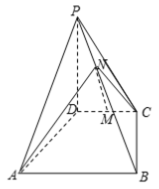
【题目】如图,四棱锥![]() 中,
中,![]() ,底面
,底面![]() 是梯形,AB∥CD,
是梯形,AB∥CD,![]() ,AB=PD=4,CD=2,
,AB=PD=4,CD=2,![]() ,M为CD的中点,N为PB上一点,且
,M为CD的中点,N为PB上一点,且![]() .
.
(1)若![]() MN∥平面PAD;
MN∥平面PAD;
(2)若直线AN与平面PBC所成角的正弦值为![]() ,求异面直线AD与直线CN所成角的余弦值.
,求异面直线AD与直线CN所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且两焦点与短轴的一个顶点的连线构成等腰直角三角形.
,且两焦点与短轴的一个顶点的连线构成等腰直角三角形.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() ,
,![]() 两点,试问:是否存在一个定点
两点,试问:是否存在一个定点![]() ,使得以
,使得以![]() 为直径的圆恒过点
为直径的圆恒过点![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现将甲、乙、丙、丁四个人安排到座位号分别是![]() 的四个座位上,他们分别有以下要求,
的四个座位上,他们分别有以下要求,
甲:我不坐座位号为![]() 和
和![]() 的座位;
的座位;
乙:我不坐座位号为![]() 和
和![]() 的座位;
的座位;
丙:我的要求和乙一样;
丁:如果乙不坐座位号为![]() 的座位,我就不坐座位号为
的座位,我就不坐座位号为![]() 的座位.
的座位.
那么坐在座位号为![]() 的座位上的是( )
的座位上的是( )
A. 甲B. 乙C. 丙D. 丁
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假定生男孩和生女孩是等可能的,令![]() {一个家庭中既有男孩又有女孩},
{一个家庭中既有男孩又有女孩},![]() {一个家庭中最多有一个女孩}.对下述两种情形,讨论
{一个家庭中最多有一个女孩}.对下述两种情形,讨论![]() 与
与![]() 的独立性.
的独立性.
(1)家庭中有两个小孩;
(2)家庭中有三个小孩.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某中学联盟举行了一次“盟校质量调研考试”活动,为了解本次考试学生的某学科成绩情况,从中抽取部分学生的分数(满分为![]() 分,得分取正整数,抽取学生的分数均在
分,得分取正整数,抽取学生的分数均在![]() 之内)作为样本(样本容量为
之内)作为样本(样本容量为![]() )进行统计,按照
)进行统计,按照![]() 的分组作出频率分布直方图,并作出样本分数的茎叶图(茎叶图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(茎叶图中仅列出了得分在![]() 的数据)
的数据)

(Ⅰ)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(Ⅱ)在选取的样本中,从成绩在![]() 分以上(含
分以上(含![]() 分)的学生中随机抽取
分)的学生中随机抽取![]() 名学生参加“省级学科基础知识竞赛”,求所抽取的
名学生参加“省级学科基础知识竞赛”,求所抽取的![]() 名学生中恰有一人得分在
名学生中恰有一人得分在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高尔顿(钉)板是在一块竖起的木板上钉上一排排互相平行、水平间隔相等的圆柱形铁钉(如图),并且每一排钉子数目都比上一排多一个,一排中各个钉子恰好对准上面一排两相邻铁钉的正中央.从入口处放入一个直径略小于两颗钉子间隔的小球,当小球从两钉之间的间隙下落时,由于碰到下一排铁钉,它将以相等的可能性向左或向右落下,接着小球再通过两铁钉的间隙,又碰到下一排铁钉.如此继续下去,在最底层的5个出口处各放置一个容器接住小球.

(Ⅰ)理论上,小球落入4号容器的概率是多少?
(Ⅱ)一数学兴趣小组取3个小球进行试验,设其中落入4号容器的小球个数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”.为了了解人们]对“延迟退休年龄政策”的态度,责成人社部进行调研.人社部从网上年龄在15![]() 65岁的人群中随机调查100人,调査数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
65岁的人群中随机调查100人,调査数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
年龄 |
|
|
|
|
|
支持“延迟退休”的人数 | 15 | 5 | 15 | 28 | 17 |
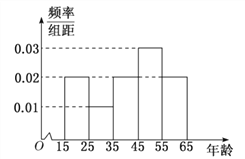
(1)由以上统计数据填![]() 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异;
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异;
45岁以下 | 45岁以上 | 总计 | |
支持 | |||
不支持 | /td> | ||
总计 |
(2)若以45岁为分界点,从不支持“延迟退休”的人中按分层抽样的方法抽取8人参加某项活动.现从这8人中随机抽2人
①抽到1人是45岁以下时,求抽到的另一人是45岁以上的概率.
②记抽到45岁以上的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com