
【题目】工厂抽取了在一段时间内生产的一批产品,测量一项质量指标值,绘制了如图所示的频率分布直方图.
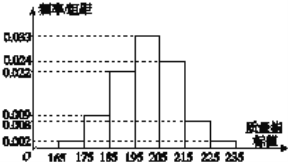
(1)计算该样本的平均值![]() ,方差
,方差![]() ;(同一组中的数据用该组区间的中点值作代表)
;(同一组中的数据用该组区间的中点值作代表)
(2)若质量指标值在![]() 之内为一等品.
之内为一等品.
(i)用样本估计总体,问该工厂一天生产的产品是否有![]() 以上为一等品?
以上为一等品?
(ii)某天早上、下午分别抽检了50件产品,完成下面的表格,并根据已有数据,判断是否有![]() 的把握认为一等品率与生产时间有关?
的把握认为一等品率与生产时间有关?
一等品个数 | 非一等品个数 | 总计 | |
早上 | 36 | 50 | |
下午 | 26 | 50 | |
总计 |
附:![]() .
.
| 0.25 | 0.15 | 0.10 | 0.050 | 0.010 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 6.635 | 10.828 |
参考数据:![]() .
.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在底面为梯形的四棱锥S﹣ABCD中,已知AD∥BC,∠ASC=60°,![]() ,SA=SC=SD=2.
,SA=SC=SD=2.
(1)求证:AC⊥SD;
(2)求三棱锥B﹣SAD的体积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个结论:
①在回归分析模型中,残差平方和越大,说明模型的拟合效果越好;
②某学校有男教师60名、女教师40名,为了解教师的体育爱好情况,在全体教师中抽取20名调查,则宜采用的抽样方法是分层抽样;
③线性相关系数![]() 越大,两个变量的线性相关性越弱;反之,线性相关性越强;
越大,两个变量的线性相关性越弱;反之,线性相关性越强;
④在回归方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 增加0.5个单位.
增加0.5个单位.
其中正确的结论是( )
A. ①②B. ①④
C. ②③D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个结论:
①在回归分析模型中,残差平方和越大,说明模型的拟合效果越好;
②某学校有男教师60名、女教师40名,为了解教师的体育爱好情况,在全体教师中抽取20名调查,则宜采用的抽样方法是分层抽样;
③线性相关系数![]() 越大,两个变量的线性相关性越弱;反之,线性相关性越强;
越大,两个变量的线性相关性越弱;反之,线性相关性越强;
④在回归方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 增加0.5个单位.
增加0.5个单位.
其中正确的结论是( )
A. ①②B. ①④
C. ②③D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的一元二次函数f(x)=ax2﹣2bx+8.
(1)设集合P={1,2,3}和Q={2,3,4,5},分别从集合P和Q中随机取一个数作为a和b,求函数y=f(x)在区间(﹣∞,2]上有零点且为减函数的概率?
(2)设集合P=[1,3]和Q[2,5],分别从集合P和Q中随机取一个实数作为a和b,求函数y=f(x)在区间(﹣∞,2]上有零点且为减函数的概率?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是20,接下来的两项是20,21,再接下来的三项是20,21,22,依此类推.求满足如下条件的最小整数N:N>100且该数列的前N项和为2的整数幂.那么该款软件的激活码是
A. 440B. 330
C. 220D. 110
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com