
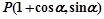 ,参数
,参数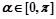 ,点Q在曲线C:
,点Q在曲线C: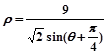 上.
上.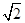 -1.
-1. 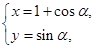 得点P的轨迹方程 (x-1)2+y2=1(y≥0), 又由又由
得点P的轨迹方程 (x-1)2+y2=1(y≥0), 又由又由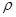 =
=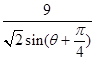 ,可得极坐标方程。
,可得极坐标方程。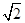 ,因此两点距离的最小值为点到直线的距离减去圆的半径。
,因此两点距离的最小值为点到直线的距离减去圆的半径。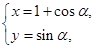 得点P的轨迹方程 (x-1)2+y2=1(y≥0),
得点P的轨迹方程 (x-1)2+y2=1(y≥0), 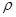 =
=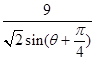 ,得
,得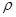 =
=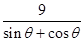 , ∴
, ∴ 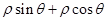 =9.
=9.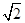 ,所以|PQ|min=4
,所以|PQ|min=4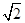 -1.
-1. 

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com