
某联欢晚会举行抽奖活动,举办方设置了甲.乙两种抽奖方案,方案甲的中奖率为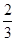 ,中将可以获得2分;方案乙的中奖率为
,中将可以获得2分;方案乙的中奖率为 ,中将可以得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中将与否互不影响,晚会结束后凭分数兑换奖品.
,中将可以得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中将与否互不影响,晚会结束后凭分数兑换奖品.
(1)若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为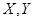 ,求
,求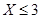 的概率;
的概率;
(2)若小明.小红两人都选择方案甲或方案乙进行抽奖,问:他们选择何种方案抽奖,累计的得分的数学期望较大?
科目:高中数学 来源: 题型:解答题
为了对某课题进行研究,用分层抽样方法从三所科研单位A、B、C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人):
| 科研单位 | 相关人数 | 抽取人数 |
| A | 16 | 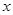 |
| B | 12 | 3 |
| C | 8 | 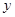 |
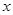 与
与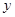 的值;
的值;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
随着经济的发展,人们生活水平的提高,中学生的营养与健康问题越来越得到学校与家长的重视. 从学生体检评价报告单了解到某校3000名学生的体重发育评价情况,得右表:
| | 偏瘦 | 正常 | 肥胖 |
| 女生(人) | 300 | 865 |  |
| 男生(人) | 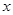 | 885 | 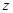 |
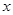 的值;
的值;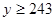 ,
,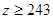 ,求肥胖学生中男生不少于女生的概率.
,求肥胖学生中男生不少于女生的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 箱中有3个黑球,6个白球,每个球被取到的概率相同,
箱中有3个黑球,6个白球,每个球被取到的概率相同,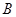 箱中没有球.我们把从
箱中没有球.我们把从 箱中取1个球放入
箱中取1个球放入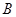 箱中,然后在
箱中,然后在 箱中补上1个与取走的球完全相同的球,称为一次操作,这样进行三次操作.
箱中补上1个与取走的球完全相同的球,称为一次操作,这样进行三次操作.
(1)分别求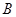 箱中恰有1个、2个、3个白球的概率;
箱中恰有1个、2个、3个白球的概率;
(2)从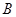 箱中一次取出2个球,记白球的个数为
箱中一次取出2个球,记白球的个数为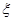 ,求
,求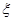 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
根据以往资料统计,大学生购买某品牌平板电脑时计划采用分期付款的期数ζ的分布列为
| ζ | 1 | 2 | 3 |
| P | 0.4 | 0.25 | 0.35 |
 ;采用3期付款的只能改为2期,概率为
;采用3期付款的只能改为2期,概率为 .数码城销售一台该平板电脑,实际付款期数
.数码城销售一台该平板电脑,实际付款期数 与利润
与利润 (元)的关系为
(元)的关系为 | 1 | 2 | 3 |
| η | 200 | 250 | 300 |
 的分布列及期望E(
的分布列及期望E( ).
).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了对某课题进行研究,用分层抽样的方法从 三所高校的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人).
三所高校的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人).
| 高校 | 相关人数 | 抽取人数 |
 | 18 |  |
 | 36 |  |
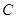 | 54 |  |
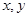 ;
;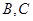 抽取的人中选2人作专题发言,求这2人都来自高校
抽取的人中选2人作专题发言,求这2人都来自高校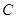 的概率.
的概率. 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两人玩猜数字游戏,规则如下:
①连续竞猜 次,每次相互独立;
次,每次相互独立;
②每次竟猜时,先由甲写出一个数字,记为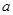 ,再由乙猜测甲写的数字,记为
,再由乙猜测甲写的数字,记为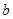 ,已知
,已知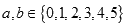 ,若
,若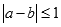 ,则本次竞猜成功;
,则本次竞猜成功;
③在 次竞猜中,至少有
次竞猜中,至少有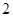 次竞猜成功,则两人获奖.
次竞猜成功,则两人获奖.
(Ⅰ) 求甲乙两人玩此游戏获奖的概率;
(Ⅱ)现从 人组成的代表队中选
人组成的代表队中选 人参加此游戏,这
人参加此游戏,这 人中有且仅有
人中有且仅有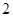 对双胞胎,记选出的
对双胞胎,记选出的 人中含有双胞胎的对数为
人中含有双胞胎的对数为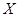 ,求
,求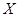 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月15日中的某一天到达该市,并停留2天.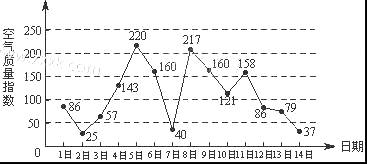
(Ⅰ)求此人到达当日空气质量优良的概率;
(Ⅱ)求此人在该市停留期间只有1天空气重度污染的概率;
(Ⅲ)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
数学试题中有12道单项选择题,每题有4个选项。某人对每道题都随机选其
中一个答案(每个选项被选出的可能性相同),求答对多少题的概率最大?并求出此种情况下概
率的大小.(可保留运算式子)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com