
| a |
| b |
| a |
| b |
| p |
| 8 |
| π |
| m |
| 1 |
| 2 |
| n |
| π |
| 4 |
| 1 |
| 2 |
| p |
| m |
| n |
| OQ |
| m |
| OP |
| n |
| p |
| m |
| p |
| m |
| n |
| OQ |
| m |
| OP |
| n |
| p |
| 8 |
| π |
| m |
| 1 |
| 2 |
| p |
| m |
| 4 |
| π |
| n |
| π |
| 4 |
| 1 |
| 2 |
| p |
| m |
| n |
| 4 |
| π |
| π |
| 4 |
| 1 |
| 2 |
| p |
| m |
| n |
| OP |
| OQ |
| OQ |
| m |
| OP |
| n |
| 1 |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
|
| π |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 2 |


科目:高中数学 来源: 题型:
| 9 |
| 5 |
| x2 |
| 25 |
| y2 |
| 9 |
| A、充要条件 |
| B、必要不充分条件 |
| C、充分不必要条件 |
| D、既非充分也非必要 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| a |
| b |
| x1+y1 |
| x2+y2 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年莱阳一中学段检测)(14分)
已知函数![]() ,
,![]() (a>0且a
(a>0且a![]() 1),其中
1),其中![]() 为常数.如果
为常数.如果
h(x)=f(x)+g(x)是增函数,且h(x)的导函数h![]() (x)存在零点.
(x)存在零点.
(1)求a的值;
(2)设A(x1、y1)、B(x2、y2)(x1 < x2)是函数y=g(x)的图象上两点,![]()
(g![]() (x)为g(x)的导函数),证明:x1 < x0 < x2
(x)为g(x)的导函数),证明:x1 < x0 < x2
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河北省高三上学期期末考试文科数学 题型:解答题
.(本题满分12分)
设A(x1,y1),B(x2,y2),是椭圆 +
+ =(a>b>0)上的两点,已知向量m=(
=(a>b>0)上的两点,已知向量m=( ,
, ),n=(
),n=( ,
, ),若m·n=0且椭圆的离心率e=
),若m·n=0且椭圆的离心率e=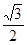 ,短轴长为2,O为坐标原点.
,短轴长为2,O为坐标原点.
(Ⅰ)求椭圆的方程;
(Ⅱ)试问:△AOB的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com