
����Ŀ��ij��������˾Ϊ��ȷ����һ���ȵ�ǰ�ڹ��Ͷ��ƻ����ռ��˽�![]() ���¹��Ͷ����
���¹��Ͷ����![]() ����λ����Ԫ��������
����λ����Ԫ��������![]() ����λ����Ԫ�����������±���
����λ����Ԫ�����������±���
�·� |
|
|
|
|
|
|
���Ͷ���� |
|
|
|
|
|
|
���� |
|
|
|
|
|
|
���Ƿֱ�������ģ�͢�![]() ����
����![]() �ֱ������ϣ��õ���Ӧ�Ļع鷽�̲����вв�������õ���ͼ��ʾ�IJв�ͼ��һЩͳ������ֵ��
�ֱ������ϣ��õ���Ӧ�Ļع鷽�̲����вв�������õ���ͼ��ʾ�IJв�ͼ��һЩͳ������ֵ��
|
|
|
|
|
|
|
|
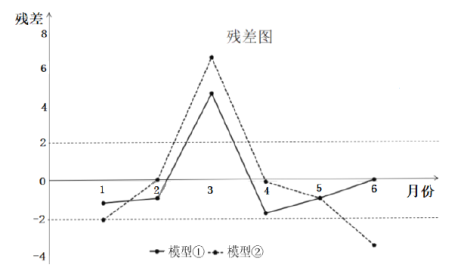
�����ݲв�ͼ���Ƚ�ģ�͢����ڵ����Ч����Ӧѡ���ĸ�ģ�ͣ���˵��������
���в����ֵ����![]() �����ݱ���Ϊ���쳣���ݣ���Ҫ����
�����ݱ���Ϊ���쳣���ݣ���Ҫ����
���������쳣���ݺ������������ѡģ�͵Ļع鷽����
�����������Ͷ����![]() ʱ����ģ�������Ԥ��ֵ�Ƕ�����
ʱ����ģ�������Ԥ��ֵ�Ƕ�����
��������һ������![]() ��
��![]() ��������
��������![]() ����ع�ֱ��
����ع�ֱ��![]() ��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ��
��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ��
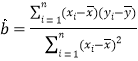
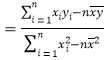 ��
��![]() .
.
���𰸡���1��Ӧ��ѡ��ģ�͢������ɼ�������2��������![]() ������
������![]()
��������
��1����������֪ģ�͢ٲв��ȽϾ��ȵ�����ˮƽ�Ĵ�״�����У����ɡ���2����i�����ûع�ֱ�߲������㷽�����ֱ�õ�![]() ���������̣����ɡ���ii����
���������̣����ɡ���ii����![]() ����ع鷽�̣������������ɡ�
����ع鷽�̣������������ɡ�
����Ӧ��ѡ��ģ�͢�����Ϊģ�͢ٲв��ȽϾ��ȵ�����ˮƽ�Ĵ�״�����У�˵��ģ
����Ͼ���Խ�ߣ��ع鷽�̵�Ԥ������Խ��.
���������������쳣���ݣ����·�Ϊ![]() �����ݺ�
�����ݺ�
![]() ��
��
![]() .
.
![]() ��
��
![]() .
.
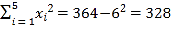
![]()
![]() ��
��
![]() ��
��
����![]() ����
����![]() �����Իع鷽��Ϊ��
�����Իع鷽��Ϊ��![]() .
.
��������![]() ����ع鷽�̵���
����ع鷽�̵���![]() ��
��
��Ԥ��ֵԼΪ![]() ��Ԫ.
��Ԫ.


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������![]() �������ⳤ��Ϊ2��
�������ⳤ��Ϊ2�� ![]() ��
�� ![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
��![]() ���е㣮
���е㣮

��1��֤���� ![]() ƽ��
ƽ��![]() ��
��
��2�����![]() ��ƽ��
��ƽ��![]() �ľ���.
�ľ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() ����֪��Բ
����֪��Բ![]() ����
����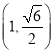 �������ҽ���ֱ�Ϊ
�������ҽ���ֱ�Ϊ![]() ��������Ϊ
��������Ϊ![]() .
.
��1������ԲE�ķ��̣�
��2����A��B�ֱ�Ϊ��ԲE�����Ҷ��㣬����M����![]() ����MA����ԲE�ڵ�P.
����MA����ԲE�ڵ�P.
��i����֤��![]() Ϊ��ֵ��
Ϊ��ֵ��
��ii����PB����PMΪֱ����Բ����һ����ΪQ���ʣ�ֱ��MQ�Ƿ�����㣬��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣�����б������õ�ˮƽ���õ�![]() ��ֱ��ͼ
��ֱ��ͼ![]() ������
������![]() �ᣬ
�ᣬ![]() ��.��
��.��![]() ����
����![]() �����Ϊ
�����Ϊ![]() ��
��![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��ִ����ͼ�ڵĿ�ͼ�������
��ִ����ͼ�ڵĿ�ͼ�������![]() ��ֵ
��ֵ
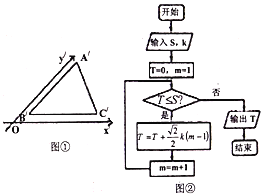
A. 12B. 10C. 9D. 6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ִ����ͼ��ʾ�ij����ͼ������![]() Ϊ������λ���������
Ϊ������λ���������![]() ��ֵ�ǣ� ��
��ֵ�ǣ� ��
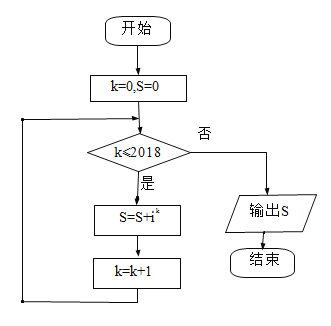
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������{an}����a1��1��a2��1��an+2��an+an+1���������{an}Ϊ쳲��������У�쳲������������Ǹ���쳲��������л��������������ߣ���Ȼ���д�������쳲����������ߵ�ͼ��������Ȼ���������ľ���ƽ����.��ͼ����������쳲�������Ϊ�ߵ�������ƴ�ɵij������л�һ��Բ�Ľ�Ϊ90�������Σ��������Ļ��߾���쳲����������ߣ���ͼ��ʾ��7�������εı߳��ֱ�Ϊa1��a2������a7���ڳ�����ABCD����ȡһ�㣬��õ㲻���κ�һ�������ڵĸ���Ϊ�� ��
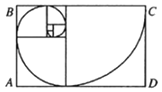
A.1![]() B.1
B.1![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() .
.
��1����![]() ���������ʵ��a��ȡֵ��Χ��
���������ʵ��a��ȡֵ��Χ��
��2��������x�ķ���![]() ��������ͬ�Ľ⣬��ʵ��a��ȡֵ��Χ.
��������ͬ�Ľ⣬��ʵ��a��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ں���f��x���������壺��f����x���Ǻ���y��f��x���ĵ�����f����x���Ǻ���f����x���ĵ�����������f����x����0��ʵ����x0����Ƶ㣨x0��f��x0����Ϊ����y��f��x�������յ�����ijͬѧ����̽�����֣��κ�һ�����κ���f��x����ax3+bx2+cx+d��a��0���������յ������κ�һ�����κ������жԳ����ģ������յ������ǶԳ����ģ���������![]() �������������̽�����������f��
�������������̽�����������f��![]() ��+f��
��+f��![]() ��+f��
��+f��![]() ��+����+f��
��+����+f��![]() ����_____��
����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������P��ABCD�У�����ABCD�DZ߳�Ϊ4�������Σ���PAD��һ���������Σ���ƽ��PAD��ƽ��ABCD����������������ı����Ϊ_____.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com