
在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.
(1)求证:EF∥平面CB1D1;
(2)求证:平面CAA1C1⊥平面CB1D1

(1)见解析(2)见解析
【解析】本题主要考查线面平行的判定定理和线面垂直的判定定理.考查对基础知识的综合应用能力和基本定理的掌握能力。
(Ⅰ)欲证EF∥平面CB1D1,根据直线与平面平行的判定定理可知只需证EF与平面CB1D1内一直线平行,连接BD,根据中位线可知EF∥BD,则EF∥B1D1,又B1D1⊂平面CB1D1,EF⊄平面CB1D1,满足定理所需条件;
(Ⅱ)欲证平面CAA1C1⊥平面CB1D1,根据面面垂直的判定定理可知在平面CB1D1内一直线与平面CAA1C1垂直,而AA1⊥平面A1B1C1D1,B1D1⊂平面A1B1C1D1,则AA1⊥B1D1,A1C1⊥B1D1,满足线面垂直的判定定理则B1D1⊥平面CAA1C1,而B1D1⊂平面CB1D1,满足定理所需条件.
解:(1)证明:连结BD.
在长方体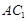 中,对角线
中,对角线 .
.
又 E、F为棱AD、AB的中点,
E、F为棱AD、AB的中点,
 .
.
 .
.
又B1D1 平面
平面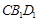 ,
,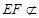 平面
平面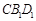 ,
,
 EF∥平面CB1D1.
EF∥平面CB1D1.
(2) 在长方体
在长方体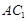 中,AA1⊥平面A1B1C1D1,而B1D1
中,AA1⊥平面A1B1C1D1,而B1D1 平面A1B1C1D1,
平面A1B1C1D1,
 AA1⊥B1D1.
AA1⊥B1D1.
又 在正方形A1B1C1D1中,A1C1⊥B1D1,
在正方形A1B1C1D1中,A1C1⊥B1D1,
 B1D1⊥平面CAA1C1.
B1D1⊥平面CAA1C1.
又 B1D1
B1D1 平面CB1D1,
平面CB1D1,
 平面CAA1C1⊥平面CB1D1.
平面CAA1C1⊥平面CB1D1.


科目:高中数学 来源: 题型:
(本小题满分12分)
在正方体ABCD-A′B′C′D′中,点M是棱AA′的中点,点O是对角线BD′的中点.
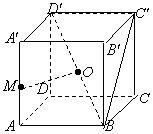
 (Ⅰ)求证:OM为异面直线AA′和BD′的公垂线;
(Ⅰ)求证:OM为异面直线AA′和BD′的公垂线;
(Ⅱ)求二面角M-BC′-B′的大小;
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
在正方体ABCD-A′B′C′D′中,点M是棱AA′的中点,点O是对角线BD′的中点.
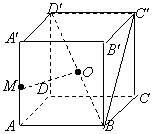
 (Ⅰ)求证:OM为异面直线AA′和BD′的公垂线;
(Ⅰ)求证:OM为异面直线AA′和BD′的公垂线;
(Ⅱ)求二面角M-BC′-B′的大小;
查看答案和解析>>
科目:高中数学 来源:2010年高考试题(四川卷)解析版(文) 题型:解答题
在正方体ABCD-A′B′C′D′中,点M是棱AA′的中点,点O是对角线BD′的中点.
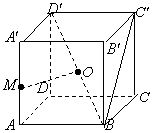
 (Ⅰ)求证:OM为异面直线AA′和BD′的公垂线;
(Ⅰ)求证:OM为异面直线AA′和BD′的公垂线;
(Ⅱ)求二面角M-BC′-B′的大小;
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com