
【题目】设![]() 、
、![]() 为平面上两个点集,满足
为平面上两个点集,满足![]() ,
,![]() ,且任意三点不共线.在集合
,且任意三点不共线.在集合![]() 和
和![]() 间各连若干条线段,每条线段均一个端点在集合
间各连若干条线段,每条线段均一个端点在集合![]() 中,另一个端点在集合
中,另一个端点在集合![]() 中,且任意两点间至多连一条线段,记所有线段构成的集合为
中,且任意两点间至多连一条线段,记所有线段构成的集合为![]() .若集合
.若集合![]() 满足对于集合
满足对于集合![]() 或
或![]() 中任意一点均至少连出
中任意一点均至少连出![]() 条线段,则称集合
条线段,则称集合![]() 是“
是“![]() 一好的”.试确定
一好的”.试确定![]() 的最大值,使得去掉任意一条线段,集合
的最大值,使得去掉任意一条线段,集合![]() 均不是
均不是![]() 一好的.
一好的.
【答案】见解析
【解析】
设集合![]() 中有
中有![]() 个点引出边数不为
个点引出边数不为![]() 条,有
条,有![]() 个点恰引出
个点恰引出![]() 条边,设集合
条边,设集合![]() 中有
中有![]() 个点引出边数不为
个点引出边数不为![]() 条,有
条,有![]() 个点恰引出
个点恰引出![]() 条边.
条边.
由于对称性,不妨设![]() .
.
记![]() ,其中,
,其中,![]() 为集合
为集合![]() 中所有恰引出
中所有恰引出![]() 条线段的点构成的集合,
条线段的点构成的集合,![]() 为集合
为集合![]() 中除去
中除去![]() 外余下的点构成的集合,记B=
外余下的点构成的集合,记B=![]() ,其中,
,其中,![]() 为集合
为集合![]() 中所有恰引出
中所有恰引出![]() 条线段的点构成的集合,
条线段的点构成的集合,![]() 为集合
为集合![]() 中除去
中除去![]() 外余下的点构成的集合.
外余下的点构成的集合.
则![]() 满足以下两个估计:
满足以下两个估计:
(1) ![]() .
.
注意到,集合![]() 中的点仅能与集合
中的点仅能与集合![]() 中的点相邻,故对于
中的点相邻,故对于![]() ,
,
![]() .
.
(2)![]() .
.
对于集合![]() 中的任意一条边,至少有一个端点在集合
中的任意一条边,至少有一个端点在集合![]() 或
或![]() 内,因此,
内,因此,
![]() .
.
由(1)、(2)知
![]()
![]() .
.
若![]() ,则
,则![]() ;
;
若![]() ,则
,则![]() .
.
故当![]() 时,
时,
![]() ;
;
当![]() 时,
时,![]() ,即
,即
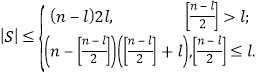
构造:(i)若![]() ,构造两个完全的二部图
,构造两个完全的二部图![]() ,即将集合
,即将集合![]() 中的点划分为两个集合
中的点划分为两个集合![]() 、
、![]() ;将集合
;将集合![]() 中的点划分为两个集合
中的点划分为两个集合![]() 、
、![]() ,
,![]() ,其中,将集合
,其中,将集合![]() 中每一点与集合
中每一点与集合![]() 中每一点均连线,将集合
中每一点均连线,将集合![]() 中每一点和集合
中每一点和集合![]() 中每一点均连线.
中每一点均连线.
(ii)若![]() ,对集合
,对集合![]() 、
、![]() 进行如下的划分:
进行如下的划分:
![]() ,
,
![]() ,
,![]() ;
;
![]() ,
,
![]() ,
,![]() .
.
此时,将集合![]() 中的每一点与集合
中的每一点与集合![]() 中的每一点相连,将集合
中的每一点相连,将集合![]() 中的每一点与集合
中的每一点与集合![]() i中的每一点均相连.然后,在
i中的每一点均相连.然后,在![]() 和
和![]() 这两个点集间再构造一个
这两个点集间再构造一个![]() 的二部正则图即可.
的二部正则图即可.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以平面直角坐标系![]() 的原点为极点,
的原点为极点, ![]() 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线
轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线![]() 的参数方程为
的参数方程为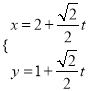 ,圆
,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与圆
的普通方程与圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 与直线
与直线![]() 交于
交于![]() 两点,若
两点,若![]() 点的直角坐标为
点的直角坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设整数![]() ,对置于
,对置于![]() 个点
个点![]() 及点
及点![]() 处的卡片作如下操作:操作
处的卡片作如下操作:操作![]() :若某个点
:若某个点![]() 处的卡片数不少于3,则可从中取出三张,在三点
处的卡片数不少于3,则可从中取出三张,在三点![]() 、
、![]() 、
、![]() 处各放一张
处各放一张![]() ;操作
;操作![]() :若点
:若点![]() 处的卡片数不少于
处的卡片数不少于![]() ,则可从中取出
,则可从中取出![]() 张,在
张,在![]() 个点
个点![]() 处各放一张。证明:只要放置于这
处各放一张。证明:只要放置于这![]() 个点处的卡片总数不少于
个点处的卡片总数不少于![]() ,则总能通过若干次操作,使得每个点处的卡片数均不少于
,则总能通过若干次操作,使得每个点处的卡片数均不少于![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用0,1,2,3,4,5这六个数字,完成下面三个小题.
(1)若数字允许重复,可以组成多少个不同的五位偶数;
(2)若数字不允许重复,可以组成多少个能被5整除的且百位数字不是3的不同的五位数;
(3)若直线方程![]() 中的a,b可以从已知的六个数字中任取2个不同的数字,则直线方程表示的不同直线共有多少条?
中的a,b可以从已知的六个数字中任取2个不同的数字,则直线方程表示的不同直线共有多少条?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}满足an+1+(-1)n an =2n-1,则{an}的前64项和为( )
A. 4290 B. 4160 C. 2145 D. 2080
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1为某省2018年1~4月快递业务量统计图,图2是该省2018年1~4月快递业务收入统计图,下列对统计图理解错误的是( )


A. 2018年1~4月的业务量,3月最高,2月最低,差值接近2000万件
B. 2018年1~4月的业务量同比增长率均超过50%,在3月底最高
C. 从两图来看,2018年1~4月中的同一个月的快递业务量与收入的同比增长率并不完全一致
D. 从1~4月来看,该省在2018年快递业务收入同比增长率逐月增长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com