练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图所示的折线表示某汽车在20秒内的速度变化情况，则该汽车在20秒内的平均速度为
    41
    41
    （m/s）．
    分析：平均速度可由公式总路程除以总时间求得，故可由图象求出总路程，由于本题中的图象是时间-速度图象，折线与X轴所围成的面积大小即为总路程的大小，总时间已知，再利用公式
    总路程
    总时间
    计算出平均速度即可．
    解答：解：由于本题中的图象是时间-速度图象，折线与X轴所围成的面积大小即为总路程的大小，
    由图知，总路程为
    1
    2
    ×2×60+
    1
    2
    ×14×
    60+100
    2
    +
    1
    2
    ×4×100    =820
    故平均速度为
    820
    20
    =41
    故答案为 41
    点评：本题是一个图象题，理解图象的意义是解题的关键，本题中理解路程与图象中多边形的面积的对应是重点，本题考查了数形结合的思想
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    某公司是一家专做产品A的国内外销售的企业，每一批产品A上市销售40天全部售完，该公司对第一批产品A上市后的国内外市场的销售情况进行了跟踪调查，调查结果如图1、图2、图3所示，其中图1中的折线表示的是国内市场的日销售量与上市时间的关系；图2中的抛物线表示国外市场的日销售量与上市时间的关系；图3中的折线表示的是每件产品A的销售利润与上市时间的关系（国内外市场相同）
    （1）分别写出国内市场的日销售量f（t），国外市场的日销售量g（t）与第一批产品A的上市时间t的关系式；
    （2）每一批产品A上市后，问哪一天这家公司的日销售利润最大？最大是多少？
    精英家教网

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    由一个小区历年市场行情调查得知，某一种蔬菜在一年12个月内每月销售量P（t）（单位：吨）与上市时间t（单位：月）的关系大致如图（1）所示的折线ABCDE表示，销售价格Q（t）（单位：元/千克）与上市时间t（单位：月）的大致关系如图（2）所示的抛物线段GHR表示（H为顶点）．
    （Ⅰ）请分别写出P（t），Q（t）关于t的函数关系式，并求出在这一年内3到6月份的销售额最大的月份？
    （Ⅱ）图（1）中由四条线段所在直线 围成的平面区域为M，动点P（x，y）在M内（包括边界），求z=x-5y的最大值；
    （Ⅲ） 由（Ⅱ），将动点P（x，y）所满足的条件及所求的最大值由加法运算类比到乘法运算（如1≤2x-3y≤3类比为1≤
    x2y3
    ≤3    ），试列出P（x，y）所满足的条件，并求出相应的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    如图所示的折线表示某汽车在20秒内的速度变化情况，则该汽车在20秒内的平均速度为________（m/s）．

    查看答案和解析>>

    科目：高中数学 来源：江苏省模拟题 题型：解答题

    由一个小区历年市场行情调查得知，某一种蔬菜在一年12个月内每月销售量（单位：吨）与上市时间（单位：月）的关系大致如图（1）所示的折线表示，销售价格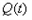（单位：元／千克）与上市时间（单位：月）的大致关系如图（2）所示的抛物线段表示（为顶点）．
    （1）请分别写出,关于的函数关系式，并求出在这一年内3到6月份的销售额最大的月份？
    （2）图（1）中由四条线段所在直线围成的平面区域为，动点在内（包括边界），求的最大值；
    (3) 由（2），将动点所满足的条件及所求的最大值由加法运算类比到乘法运算（如类比为），试列出所满足的条件，并求出相应的最大值．

                       

    查看答案和解析>>

    同步练习册答案