
【题目】已知函数f(x)=(x+1)e-x(e为自然对数的底数).
(1)求函数f(x)的单调区间;
(2)设函数φ(x)=xf(x)+tf′(x)+e-x,存在实数x1,x2∈[0,1],使得2φ(x1)<φ(x2)成立,求实数t的取值范围.
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在[-1,1]上的奇函数,在[0,1]上f(x)=2x+ln(x+1)-1.
(1)求函数f(x)的解析式;并判断f(x)在[-1,1]上的单调性(不要求证明);
(2)解不等式f(2x-1)+f(1-x2)≥0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的标准方程为
的标准方程为![]() ,
, ![]() 为抛物线
为抛物线![]() 上一动点,
上一动点, ![]() (
(![]() )为其对称轴上一点,直线
)为其对称轴上一点,直线![]() 与抛物线
与抛物线![]() 的另一个交点为
的另一个交点为![]() .当
.当![]() 为抛物线
为抛物线![]() 的焦点且直线
的焦点且直线![]() 与其对称轴垂直时,
与其对称轴垂直时, ![]() 的面积为18.
的面积为18.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)记![]() ,若
,若![]() 值与
值与![]() 点位置无关,则称此时的点
点位置无关,则称此时的点![]() 为“稳定点”,试求出所有“稳定点”,若没有,请说明理由.
为“稳定点”,试求出所有“稳定点”,若没有,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地随着经济的发展,居民收入逐年增长.该地一建设银行统计连续五年的储蓄存款(年底余额)得到下表:
年份 |
|
|
|
|
|
储蓄存款 (千亿元) |
|
|
|
|
|
为便于计算,工作人员将上表的数据进行了处理(令![]() ,
, ![]() ),得到下表:
),得到下表:
时间 |
|
|
|
|
|
储蓄存款 |
|
|
|
|
|
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(Ⅱ)通过(Ⅰ)中的方程,求出![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅲ)用所求回归方程预测到![]() 年年底,该地储蓄存款额可达多少?
年年底,该地储蓄存款额可达多少?
附:线性回归方程![]() ,其中
,其中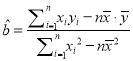 ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com