
【题目】如图,四棱锥P﹣ABCD的底面ABCD为直角梯形,AD//BC,且![]() ,BC⊥DC,∠BAD=60°,平面PAD⊥底面ABCD,E为AD的中点,△PAD为等边三角形,M是棱PC上的一点,设
,BC⊥DC,∠BAD=60°,平面PAD⊥底面ABCD,E为AD的中点,△PAD为等边三角形,M是棱PC上的一点,设![]() (M与C不重合).
(M与C不重合).
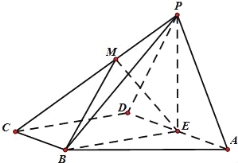
(1)求证:CD⊥DP;
(2)若PA∥平面BME,求k的值;
(3)若二面角M﹣BE﹣A的平面角为150°,求k的值.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)先证![]() 从而
从而![]() 平面
平面![]() ,进而
,进而![]() 再由
再由![]() 得到
得到![]() ,可证
,可证![]() ;(2)连接
;(2)连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() 可得
可得![]() ,从而
,从而![]() ,进而
,进而![]() 求出
求出![]() 的值;(3)连接
的值;(3)连接![]() ,做
,做![]() 交
交![]() 于
于![]() ,做
,做![]() 于
于![]() ,连
,连![]() ,则
,则![]() 为二面角的平面角,进而可求出
为二面角的平面角,进而可求出![]() 的值.
的值.
试题解析:证明:(1)因为△PAD为等边三角形,E为AD的中点,所以PE⊥AD.
因为平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,PE![]() 平面PAD,
平面PAD,
所以PE⊥平面ABCD.
又CD![]() 平面ABCD,所以PE⊥CD.
平面ABCD,所以PE⊥CD.
由已知得CD⊥DA,PE∩AD=E,所以CD⊥平面PAD.
双DP![]() 平面PAD,所以CD⊥DP.
平面PAD,所以CD⊥DP.
解:(2)连接AC交BE于N,连接MN.
因为PA∥平面BME,PA![]() 平面PAC,
平面PAC,
平面PAC∩平面BME=MN,所以PA∥MN.
因为AD∥BC,BC⊥DC,所以∠CBN=∠AEN=90°.
又CB=AE,∠CNB=∠ANE,所以△CNB≌△ANE.
所以CN=NA,则M为PC的中点,k=1.
(3)依题意,若二面角M﹣BE﹣A的大小为150°,则二面角M﹣BE﹣C的大小为30°.
连接CE,过点M作MF∥PE交CE于F,过A(0,1,0)作FG⊥BE于G,连接MG.
因为PE⊥平面ABCD,所以MF⊥平面ABCD.
又BE![]() 平面ABCD,所以MF⊥BE.
平面ABCD,所以MF⊥BE.
又MF∩FG=F,MF![]() 平面MFG,FG
平面MFG,FG![]() 平面MFG,
平面MFG,
所以BE⊥平面MFG,从而BE⊥MG.
则∠MGF为二面角M﹣BE﹣C的平面角,即∠MGF=30°.
在等边△PAD中,![]() .由于
.由于![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() .
.
在△MFG中,![]()
解得k=3.


科目:高中数学 来源: 题型:
【题目】如图,正三棱柱![]() 各条棱的长度均相等,
各条棱的长度均相等,![]() 为
为![]() 的中点,
的中点,![]() 分别是线段
分别是线段![]() 和线段
和线段![]() 的动点(含端点),且满足
的动点(含端点),且满足![]() ,当
,当![]() 运动时,下列结论中不正确的是
运动时,下列结论中不正确的是

A. 在![]() 内总存在与平面
内总存在与平面![]() 平行的线段
平行的线段
B. 平面![]() 平面
平面![]()
C. 三棱锥![]() 的体积为定值
的体积为定值
D. ![]() 可能为直角三角形
可能为直角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了选拔参加自行车比赛的选手,对自行车运动员甲、乙两人在相同条件下进行了6次测试,测得他们的最大速度(单位:m/s)的数据如下:
甲 | 27 | 38 | 30 | 37 | 35 | 31 |
乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(1)画出茎叶图,由茎叶图你能获得哪些信息;
(2)估计甲、乙两运动员的最大速度的平均数和方差,并判断谁参加比赛更合适.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】行了一次水平测试。用系统抽样的方法抽取了50名学生的数学成绩,准备进行分析和研究。经统计成绩的分组及各组的频数如下:![]() ,2;
,2;![]() ,3;
,3;![]() ,10;
,10;![]() ,15;
,15;![]() ,12;
,12;![]() ,8.
,8.
(Ⅰ)频率分布表
分组 | 频数 | 频率 |
| 2 | |
| 3 | |
| 10 | |
| 15 | |
| 12 | |
| 8 | |
合计 | 50 |
频率分布直方图为
(Ⅰ)完成样本的频率分布表;画出频率分直方图;
(Ⅱ)估计成绩在85分以下的学生比例;
(Ⅲ)请你根据以上信息去估计样本的众数、中位数、平均数.(精确到0.01)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】偶函数f(x)(x∈R)满足:f(﹣4)=f(1)=0,且在区间[0,3]与[3,+∞)上分别递减和递增,则不等式x3f(x)<0的解集为( )
A.(﹣∞,﹣4)∪(4,+∞)
B.(﹣4,﹣1)∪(1,4)
C.(﹣∞,﹣4)∪(﹣1,0)
D.(﹣∞,﹣4)∪(﹣1,0)∪(1,4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcosθ+ρsinθ=1,曲线C的极坐标方程为ρsin2θ=8cosθ.
(1)求直线l与曲线C的直角坐标方程;
(2)设点M(0,1),直线l与曲线C交于不同的两点P,Q,求|MP|+|MQ|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年世界海洋日暨全国海洋宣传日主场活动在海南三亚举行,此次活动主题为“珍惜海洋资源保护海洋生物多样性”,旨在进一步提高公众对节约利用海洋资源.保护海洋生物多样性的认识,为保护蓝色家园做出贡献.联合国于第63届联合国大会上将每年的6月8日确定为“世界海洋日”,为了响应世界海洋日的活动,2019年12月北京某高校行政主管部门从该大学随机抽取部分大学生进行一次海洋知识测试,并根据被测验学生的成绩(得分都在区间![]() 内)绘制成如图所示的频率分布直方图.
内)绘制成如图所示的频率分布直方图.
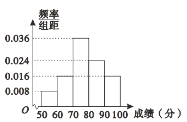
若学生的得分成绩不低于80分的认为是“成绩优秀”现在从认为“成绩优秀”的学生中根据原有分组按照分层抽样的方法抽取10人进行奖励,最后再从这10人中随机选取3人作为优秀代表发言.
(1)求所抽取的3人不属于同一组的概率;
(2)记这3人中,![]() 为测试成绩在
为测试成绩在![]() 内的人数,求
内的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com