
| A. | $\frac{5}{2}$或$\frac{3}{2}$ | B. | $\frac{3}{2}$或1 | C. | 1或$\frac{1}{2}$ | D. | $\frac{1}{2}$或$\frac{5}{2}$ |
分析 由题意利用两个向量的数量积的定义求得$\overrightarrow{a}$○$\overrightarrow{b}$的解析式,得到cos2θ=$\frac{mn}{4}$∈(0,$\frac{3}{4}$),可得整数m,n的值,从而求得$\overrightarrow{a}$○$\overrightarrow{b}$的值.
解答 解:由题意可得则$\overrightarrow{a}$○$\overrightarrow{b}$=$\frac{\overrightarrow{a}•\overrightarrow{b}}{\overrightarrow{b}•\overrightarrow{b}}$=$\frac{|\overrightarrow{a}|•|\overrightarrow{b}|}{{|\overrightarrow{b}|}^{2}}$cosθ=$\frac{|\overrightarrow{a}|}{|\overrightarrow{b}|}$cosθ=$\frac{n}{2}$,同理可得$\overrightarrow{b}$○$\overrightarrow{a}$=$\frac{|\overrightarrow{b}|}{|\overrightarrow{a}|}$cosθ=$\frac{m}{2}$,m、n∈Z.
∵θ∈($\frac{π}{6}$,$\frac{π}{2}$),∴cosθ∈(0,$\frac{\sqrt{3}}{2}$),∴cos2θ=$\frac{mn}{4}$∈(0,$\frac{3}{4}$),根据$\overrightarrow{a}$○$\overrightarrow{b}$与$\overrightarrow{b}$○$\overrightarrow{a}$都在集合{$\frac{n}{2}$|n∈Z}中,
∴m=1,n=2,或 m=2,n=1,或m=1,n=1,
∴$\overrightarrow{a}$○$\overrightarrow{b}$=1 或$\frac{1}{2}$,
故选:C.
点评 本题主要考查两个向量的数量积的定义,得到m、n∈z,且$\frac{mn}{4}$∈(0,$\frac{3}{4}$),是解题的关键,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{7}$ | B. | $\frac{1}{3}$ | C. | 0 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2π | B. | 4π | C. | 6π | D. | 8π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2-y2=1 | B. | y2-x2=1 | C. | y2-x2=2 | D. | x2-y2=2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ab<b2 | B. | a2<b2 | C. | lg(-ab)<lg(-a2) | D. | 2${\;}^{\frac{1}{b}}$<2${\;}^{\frac{1}{a}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
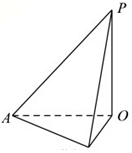 如图,有一建筑物OP,为了测量它的高度,在地面上选一长度为40m的基线AB,若在点A处测得P点的仰角为30°,在B点处的仰角为45°,且∠AOB=30°,则建筑物的高度为( )
如图,有一建筑物OP,为了测量它的高度,在地面上选一长度为40m的基线AB,若在点A处测得P点的仰角为30°,在B点处的仰角为45°,且∠AOB=30°,则建筑物的高度为( )| A. | 20m | B. | 20$\sqrt{2}$m | C. | 20$\sqrt{3}$m | D. | 40m |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 正常 | 非正常 | 合计 | |
| 男 | 30 | 20 | 50 |
| 女 | 50 | 10 | 60 |
| 合计 | 80 | 30 | 110 |
| P(K2≥k0) | 0.100 | 0.05 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com