
【题目】设圆![]() 的圆心为
的圆心为![]() ,直线
,直线![]() 过点
过点![]() 且与
且与![]() 轴不重合,
轴不重合,![]() 交圆
交圆![]() 于
于![]() 两点,过
两点,过![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() .
.
(1)证明:![]() 为定值,并写出点
为定值,并写出点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() 交
交![]() 于
于![]() 两点,
两点,![]() 为坐标原点,求
为坐标原点,求![]() 面积的取值范围.
面积的取值范围.
 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
【题目】某中学为了解高二学生对“地方历史”校本课程的喜欢是否与在本地成长有关,在全校高二学生中随机抽取了20名,得到一组不完全的统计数据如下表:
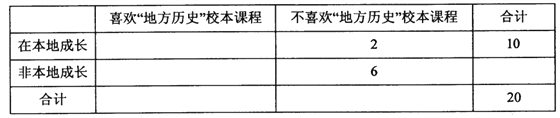
(1)补齐上表数据,并分别从被抽取的喜欢“地方历史”校本课程与不喜欢“地方历史”校本课程的学生中各选1名做进一步访谈,求至少有1名学生属于在本地成长的概率;
(2)试回答:能否在犯错误的概率不超过0.10的前提下认为“是否喜欢地方历史校本课程与在本地成长有关”.
附:

(参考公式: 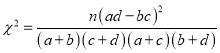 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市拟兴建九座高架桥,新闻媒体对此进行了问卷调查,在所有参与调查的市民中,持“支持”、“保留”和“不支持”态度的人数如下表所示:
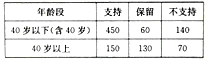
(1)在所有参与调查的人中,用分层抽样的方法抽取部分市民做进一步调研(不同态度的群体中亦按年龄分层抽样),已知从“保留”态度的人中抽取了19人,则在“支持”态度的群体中,年龄在40岁以下(含40岁)的人有多少被抽取;
(2)在持“不支持”态度的人中,用分层抽样的方法抽取6人做进一步的调研,将此6人看作一个总体,在这6人中任意选取2人,求至少有1人在40岁以上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】运货卡车以每小时![]() 千米的速度匀速行驶130千米
千米的速度匀速行驶130千米![]()
![]() (单位:千米/小时).假设汽油的价格是每升6元,而汽车每小时耗油
(单位:千米/小时).假设汽油的价格是每升6元,而汽车每小时耗油![]() 升,司机的工资是每小时30元.
升,司机的工资是每小时30元.
(1)求这次行车总费用![]() 关于
关于![]() 的表达式;
的表达式;
(2)当![]() 为何值时,这次行车的总费用最低,并求出最低费用的值.
为何值时,这次行车的总费用最低,并求出最低费用的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆x2+y2=12与抛物线x2=4y相交于A,B两点,F为抛物线的焦点,若过点F且斜率为1的直线l与抛物线和圆交于四个不同的点,从左至右依次为P1 , P2 , P3 , P4 , 则|P1P2|+|P3P4|的值 , 若直线m与抛物线相交于M,N两点,且与圆相切,切点D在劣弧 ![]() 上,则|MF|+|NF|的取值范围是 .
上,则|MF|+|NF|的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2﹣ax+a+3,g(x)=ax﹣2a.
(1)若函数h(x)=f(x)﹣g(x)在[﹣2,0]上有两个零点,求实数a的取值范围;
(2)若存在x0∈R,使得f(x0)≤0与g(x0)≤0同时成立,求实数a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)求函数f(x)的最小正周期和单调减区间;
(2)已知△ABC的三个内角A,B,C的对边分别为a,b,c,其中a=7,若锐角A满足 ![]() ,且
,且 ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com