
| A�� | $\frac{1}{3}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{\sqrt{2}}{2}$ | D�� | $\frac{2}{3}$ |
���� ����һ����ֱ�߷��̣�������Բ���̣����������ʽ���A��B�ĺ����꣬��-y1=2y2���������a��c�Ĺ�ϵ�����������ʹ�ʽ�����������Բ�������ʣ�
��������������Բ�ĵڶ����弰���������ε����ʣ����حAFح=$\frac{2}{3}$حACح��e=$\frac{حAFح}{حACح}$=$\frac{2}{3}$��
���  �⣺����һ����A��x1��y1����B��x2��y2����������֪y1��0��y2��0��
�⣺����һ����A��x1��y1����B��x2��y2����������֪y1��0��y2��0��
ֱ��l��б��k=-$\sqrt{3}$��ֱ��l����Ϊy=-$\sqrt{3}$��x-c������
����$\left\{\begin{array}{l}{y=-\sqrt{3}��x-c��}\\{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$���������3a2+b2��y2-2$\sqrt{3}$b2cy-3b4=0�����y1=$\frac{\sqrt{3}{b}^{2}��c+2a��}{3{a}^{2}+{b}^{2}}$��y2=$\frac{\sqrt{3}{b}^{2}��c-2a��}{3{a}^{2}+{b}^{2}}$��
��$\overrightarrow{AF}$=2$\overrightarrow{FB}$����-y1=2y2����-$\frac{\sqrt{3}{b}^{2}��c+2a��}{3{a}^{2}+{b}^{2}}$=2��$\frac{\sqrt{3}{b}^{2}��c-2a��}{3{a}^{2}+{b}^{2}}$��
�����ã�3c=2a��
��Բ��������e=$\frac{c}{a}$=$\frac{2}{3}$��
��ѡD
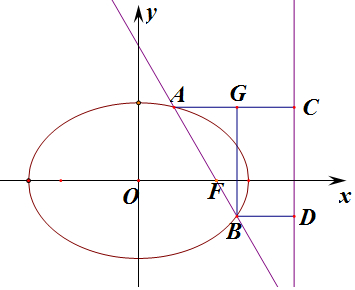
����������ͼ��������Բ������Ϊl����A����AC��l��C��
����B��BD��l��D���ٹ�B����BG��AC��G��
ֱ�ǡ�ABG�У���BAG=60�㣬��حABح=2حAGح������
����Բ�ĵڶ�����ã�e=$\frac{حAFح}{حACح}$=$\frac{حBFح}{حBDح}$��
��ح$\overrightarrow{AF}$ح=2ح$\overrightarrow{FB}$ح����حACح=2حBDح��
ֱ������ABDC�У�حAGح=حACح-حBDح=$\frac{1}{2}$حACح����
�ɢ٢ڿ�֪���ɵ�حABح=حACح��
�֡�حAFح=$\frac{2}{3}$حACح��
��e=$\frac{حAFح}{حACح}$=$\frac{2}{3}$��
��������Ϊ=$\frac{2}{3}$��
��ѡD��
���� ���⿼����Բ�����ʣ�����ֱ������Բ��λ�ù�ϵ��������Բ�ĵڶ����壬������Բ��λ�ù�ϵʱ�����㸴�ӣ�����������Բ�ĵڶ����壬���Լ��㣬��������ٶȣ������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
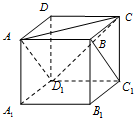 ��������ABCD-A1B1C1D1�У���ͼ������֪��P��ֱ��BC1���˶����������ĸ����⣺
��������ABCD-A1B1C1D1�У���ͼ������֪��P��ֱ��BC1���˶����������ĸ����⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | $\frac{7}{2}$ | C�� | 4 | D�� | $\frac{9}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{5}{6}��$ | B�� | $\frac{1}{3}��$ | C�� | $\frac{11}{6}��$ | D�� | $\frac{2}{3}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | $\frac{2}{3}$ | C�� | $\frac{1}{2}$ | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �������쳤��ԭ����2���������겻�䣩��������ƽ���ƶ�$\frac{��}{8}$����λ���� | |
| B�� | �������쳤��ԭ����2���������겻�䣩��������ƽ���ƶ�$\frac{��}{4}$����λ���� | |
| C�� | ���������̵�ԭ����$\frac{1}{2}$���������겻�䣩��������ƽ���ƶ�$\frac{��}{4}$����λ���� | |
| D�� | ���������̵�ԭ����$\frac{1}{2}$���������겻�䣩��������ƽ���ƶ�$\frac{��}{8}$����λ���� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com