
【题目】已知函数y=f(x)是偶函数,当x>0时,![]() ;当x∈[﹣3,﹣1]时,记f(x)的最大值为m,最小值为n,则m﹣n=________
;当x∈[﹣3,﹣1]时,记f(x)的最大值为m,最小值为n,则m﹣n=________
【答案】1
【解析】
先利用偶函数的定义:f(﹣x)=f(x),结合当x>0时,![]() 的解析式,求出函数在[﹣3,﹣1]上的解析式,再利用导数求出函数的最值即得m﹣n.
的解析式,求出函数在[﹣3,﹣1]上的解析式,再利用导数求出函数的最值即得m﹣n.
当x∈[﹣3,﹣1]时,﹣x∈[1,3]
∵当x>0时,f(x)![]()
∴f(﹣x)![]()
∵函数y=f(x)是偶函数
∴f(x)![]() ,x∈[﹣3,﹣1]
,x∈[﹣3,﹣1]
∵f′(x)=﹣1![]()
当﹣3≤x<﹣2时,f′(x)<0,函数在[﹣3,﹣2)上是减函数;当﹣2<x<﹣1时,f′(x)>0,函数在[﹣2,﹣1]上是增函数,
所以当x=﹣2时,函数有最小值4;当x=﹣3时f(﹣3)![]() ;
;
当x=﹣1时,f(﹣1)=5所以函数的最大值为5
所以m=5,n=4,
故m﹣n=1,
故答案为1.


科目:高中数学 来源: 题型:
【题目】某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场销售价与上市时间的关系用图(1)的一条折线表示;西红柿的种植成本与上市时间的关系用图(2)的抛物线段表示.


(1)写出图(1)表示的市场售价与时间的函数关系式![]() 写出图(2)表示的种植成本与时间的函数关系式
写出图(2)表示的种植成本与时间的函数关系式![]()
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿收益最大?(注:市场售价和种植成本的单位:元/![]() kg,时间单位:天.)
kg,时间单位:天.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在空间直角坐标系中有直三棱柱ABC﹣A1B1C1 , CA=CC1=2CB,则直线BC1与直线AB1夹角的余弦值为( )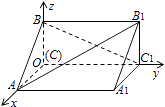
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从装有2只红球,2只白球和1只黑球的袋中逐一取球,已知每只球被抽取的可能性相同.
(Ⅰ)若抽取后又放回,抽3次.
(ⅰ)分别求恰2次为红球的概率及抽全三种颜色球的概率;
(ⅱ)求抽到红球次数![]() 的数学期望及方差.
的数学期望及方差.
(Ⅱ)若抽取后不放回,写出抽完红球所需次数![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C![]() ,直线
,直线![]() (
(![]() 为参数)
为参数)
(1)写出曲线C的参数方程和直线l的普通方程;
(2)过曲线C上任意一点P作与l夹角为30°的直线,交l于点A,求|PA|的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,AE⊥平面ABC,CD∥AE,F是BE的中点,AC=BC=1,∠ACB=90°,AE=2CD=2.
证明DF⊥平面ABE;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“石头、剪刀、布”,又称“猜丁壳”,是一种流行多年的猜拳游戏,起源于中国,然后传到日本、朝鲜等地,随着亚欧贸易的不断发展,它传到了欧洲,到了近代逐渐风靡世界.其游戏规则是:出拳之前双方齐喊口令,然后在语音刚落时同时出拳,握紧的拳头代表“石头”,食指和中指伸出代表“剪刀”,五指伸开代表“布”.“石头”胜“剪刀”、“剪刀”胜“布”、而“布”又胜过“石头”.若所出的拳相同,则为和局.小军和大明两位同学进行“五局三胜制”的“石头、剪刀、布”游戏比赛,则小军和大明比赛至第四局小军胜出的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com