已知直线l:y=2x+1和圆C:x2+y2=4,
(1)试判断直线和圆的位置关系.
(2)求过点P(-1,2)且与圆C相切的直线的方程.
解:(1)因为x
2+y
2=4,
所以圆心为(0,0),半径r=2.
又因为y=2x+1,
所以圆心到直线的距离为d=
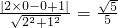
<2=r.
所以直线与圆相交.
(2)设过点P(-1,2)且与圆C相切的直线的方程为x=-1时,不合题意舍去
设过点P(-1,2)且与圆C相切的直线的方程的斜率为k,
则切线方程为kx-y+k+2=0,
由
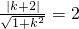
,
化简得3k
2-4k=0
解得k=0或

所以切线方程为y=0或4x-3y+10=0
分析:(1)根据圆的标准方程,找出圆心C的坐标和半径r,利用点到直线的距离公式求出圆心C到直线l的距离d,判定d与r的大小即可确定出直线l与圆C的位置关系;
(2)设过点P(-1,2)且与圆C相切的直线的方程为x=-1时,不合题意舍去;设过点P(-1,2)且与圆C相切的直线的方程的斜率为k,得出切线方程为kx-y+k+2=0,利用圆心到直线的距离等于半径列出关于k的方程,求出k值,从而得出切线方程.
点评:此题考查了直线与圆的位置关系,要求学生掌握点到直线的距离公式.圆心到直线的距离为d,圆的半径为r,当d>r时,直线与圆的位置关系为相离;当d=r时,直线与圆相切;当d<r时,直线与圆相交.

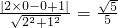 <2=r.
<2=r.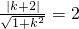 ,
,

