
����Ŀ���й����������ղ�������2019��4��29����10��7���ڱ��������������У���ί��Ϊ�����ο��������Ƴ�������Ա����������Ա�����չ��ʷ������£�
![]() �����������������
�����������������
����һ��
��н | 150Ԫ |
����ʱ�� | 6Ԫ/Сʱ |
����·�� | 11Ԫ/���� |
![]() ����������������ɣ���1�����ݹ���ʱ��20Ԫ/Сʱ�Ʒѣ���2������·�̲�����4����ʱ����10Ԫ/����Ʒѣ�����4����ʱ���������ְ�15Ԫ/����Ʒѣ���֪������Ա��ÿ���ϰ�8Сʱ�����ڸ������أ�������Ա��ÿ�����ߵ�·����һ������������������ڼ䣬��ί���ij��100��������Ա��������·��������ͳ�ƣ�Ϊ�˼��㷽���������·�̽���ȡ����������������1.8���ﰴ1������㣬����5.7���ﰴ5������㣮�����ʾ��
����������������ɣ���1�����ݹ���ʱ��20Ԫ/Сʱ�Ʒѣ���2������·�̲�����4����ʱ����10Ԫ/����Ʒѣ�����4����ʱ���������ְ�15Ԫ/����Ʒѣ���֪������Ա��ÿ���ϰ�8Сʱ�����ڸ������أ�������Ա��ÿ�����ߵ�·����һ������������������ڼ䣬��ί���ij��100��������Ա��������·��������ͳ�ƣ�Ϊ�˼��㷽���������·�̽���ȡ����������������1.8���ﰴ1������㣬����5.7���ﰴ5������㣮�����ʾ��
��������
����·�� ����� |
|
|
|
|
|
���� | 5 | 10 | 15 | 45 | 25 |
���ֱ�д�����ַ������չ���![]() ����λ��Ԫ����������·��
����λ��Ԫ����������·��![]() ����λ�����
����λ�����![]() �ĺ�����ϵ
�ĺ�����ϵ
�����ְ��շֲ�����ķ���ʽ��![]() ��
��![]() ����ȡ5����ɰ��ķ���ӣ��ٴ���5���г�ȡ3�˵�С��ñ����С��ñ��ǡ��1������
����ȡ5����ɰ��ķ���ӣ��ٴ���5���г�ȡ3�˵�С��ñ����С��ñ��ǡ��1������![]() �ĸ��ʣ�
�ĸ��ʣ�
�ڡ�����Ա��С����Ϊ����ԭ��ÿ��ֻ������12�����������չ��ʵĽǶȿ��ǣ������С��ѡ��ʹ�����ַ�����ʹ�����չ��ʸ��ߣ�
���𰸡�����![]() ������
������![]() ��
��![]() ��
��![]() ������
������![]() ������
������![]() ���ڽ���ѡ
���ڽ���ѡ![]() ����.
����.
��������
���������������ɵ����ַ������չ���![]() ��������·��
��������·��![]() �ĺ�����ϵ.
�ĺ�����ϵ.
�������оٷ��ɵû����¼�������������¼��л����¼��ĸ������Ӷ��ɵ�����ĸ���.
�� ���ã��ĺ����ɵ�С�ŵ��չ��ʣ��������ù��ʶ�Ĵ�С��ϵѡ��![]() ����.
����.
����![]() ������
������![]() ��
��![]() ��
��
![]() ������
������ ����
����![]() .
.
����������Ϊ![]() ���������
���������![]() �г�ȡ2�ˣ��ֱ���Ϊ
�г�ȡ2�ˣ��ֱ���Ϊ![]() ��
��![]() ��
��
��![]() �г�ȡ3�ˣ��ֱ���Ϊ
�г�ȡ3�ˣ��ֱ���Ϊ![]() ��
��![]() ��
��![]() .
.
�衰С��ñ��ǡ��һ������![]() ��Ϊ�¼�
��Ϊ�¼�![]() ��
��
������¼���![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��10��.
��10��.
![]() �еĻ����¼���
�еĻ����¼���![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��6�֣�����
��6�֣�����![]() .
.
��������![]() ��������
��������![]() ��
��
![]() ������
������![]() .
.
���Խ���ѡ![]() ����.
����.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���ԭ��OΪ���㣬x���������Ϊ���ᣬ����������ϵ������C�ļ����귽��Ϊ![]() ��
��
��1��������C����ͨ���̣�
��2��ֱ��l�IJ�������Ϊ![]() ����tΪ��������ֱ��l��x�ύ�ڵ�F��������C�Ľ���ΪA��B����
����tΪ��������ֱ��l��x�ύ�ڵ�F��������C�Ľ���ΪA��B����![]() ȡ��Сֵʱ����ֱ��l��ֱ�����귽�̣�
ȡ��Сֵʱ����ֱ��l��ֱ�����귽�̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ���㣺
���㣺![]() ������
������![]() ����
����![]()
![]() .����
.����![]() ���㣺
���㣺![]()
![]() .
.
��1����![]()
![]()
![]()
![]() ��ֵ��
��ֵ��
��2���������![]() ��ͨ�ʽ��
��ͨ�ʽ��
��3���ʣ�����![]() ��ÿһ���ܷ��Ϊ���������ܣ����k�����п���ֵ�������ܣ���˵������.
��ÿһ���ܷ��Ϊ���������ܣ����k�����п���ֵ�������ܣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ƶ����������Ĺ�����������Ϊ�����Ĵ�����֮һ����ʱ���ھͷ���ȫ�������������µij������飬ij����������Ӫ��˾���г��о���ԱΪ�˽˾�ľ�Ӫ״�����Ըù�˾��������µ��г�ռ����![]() ������ͳ�ƣ���������
������ͳ�ƣ���������
�·� |
|
|
|
|
|
|
�·ݴ���x | 1 | 2 | 3 | 4 | 5 | 6 |
y | 11 | 13 | 16 | 15 | 20 | 21 |
![]() �������ϵ��˵���ܷ������Իع�ģ�����y���·ݴ���x֮��Ĺ�ϵ������ܣ�������y����x�����Իع鷽�̣���Ԥ��ù�˾2018��12�µ��г�ռ����
�������ϵ��˵���ܷ������Իع�ģ�����y���·ݴ���x֮��Ĺ�ϵ������ܣ�������y����x�����Իع鷽�̣���Ԥ��ù�˾2018��12�µ��г�ռ����![]() ������ܣ���˵�����ɣ�
������ܣ���˵�����ɣ�
![]() ���ݵ������ݣ���˾�����ٲɹ�һ�����������г������вɹ��ɱ��ֱ�Ϊ1000Ԫ
���ݵ������ݣ���˾�����ٲɹ�һ�����������г������вɹ��ɱ��ֱ�Ϊ1000Ԫ![]() ����800Ԫ
����800Ԫ![]() ����A��B����ͣ�������������ͬ
����A��B����ͣ�������������ͬ![]() ���ǹ�˾�ľ���Ч�棬�ù�˾��������������п�ѧģ����ԣ��õ������ʹ������Ƶ���������
���ǹ�˾�ľ���Ч�棬�ù�˾��������������п�ѧģ����ԣ��õ������ʹ������Ƶ���������
�������� ���� | 1�� | 2�� | 3�� | 4�� | �ܼ� |
A | 10 | 30 | 40 | 20 | 100 |
B | 15 | 40 | 35 | 10 | 100 |
�����㣬ƽ��ÿ������ÿ�����Ϊ��˾��������500Ԫ![]() �����dz��ɹ��ɱ�����������ɱ�������ÿ��������ʹ���������������꣬��Ƶ�ʹ���ÿ����ʹ�������ĸ��ʣ��ֱ�����100��������������ƽ��������Ϊ�������ݣ�������Ǹù�˾�ĸ����ˣ���ѡ��ኹ��Ŀ�ͣ�
�����dz��ɹ��ɱ�����������ɱ�������ÿ��������ʹ���������������꣬��Ƶ�ʹ���ÿ����ʹ�������ĸ��ʣ��ֱ�����100��������������ƽ��������Ϊ�������ݣ�������Ǹù�˾�ĸ����ˣ���ѡ��ኹ��Ŀ�ͣ�
�ο����ݣ�![]() ��
��![]() ��
��![]()
�ο���ʽ�����ϵ��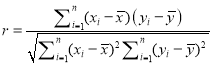
�ع�ֱ�߷���![]() �е�б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ��
�е�б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ��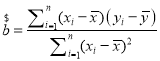 ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x����|x��2|+|x+1|��
��1���ⲻ��ʽf��x����4��
��2����f��x��+f��y����6����x+y��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ���е㣬
���е㣬![]() �ǵȱ������Σ�ƽ��
�ǵȱ������Σ�ƽ��![]() ƽ��
ƽ��![]() .
.
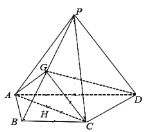
��1����֤��![]() ƽ��
ƽ��![]() ��
��
��2��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ĸ����ۣ�������ȷ����( )
�ٴ����ٴ��͵�������ˮ���ϣ�ÿ30���ӳ�ȡһ����Ʒ���м�⣬�����ij����Ƿֲ�������ڡ�![]() �������ı�Ҫ������������ǡ�
�������ı�Ҫ������������ǡ�![]() ����������������
����������������![]() ��
��![]() ������
������![]() �ı���Ϊ3����
�ı���Ϊ3����![]() ��
��![]() ������
������![]() �ķ���Ϊ145����
�ķ���Ϊ145����![]() ��
��![]() ��
��![]() �����������ɡ�
�����������ɡ�![]() ����ȵõ���
����ȵõ���![]() ���Ľ�������ȷ��.
���Ľ�������ȷ��.
A.�٢�B.�ڢ�C.�٢�D.�ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ������ABCD��A1B1C1D1������ABCD�DZ߳�Ϊ6�������Σ�M��N�ֱ�Ϊ�߶�AC1��D1C�ϵĶ��㣬��ֱ��MN��ƽ��B1BCC1û�й�������������������㣬��EΪMN���е㣬��E��Ĺ켣����Ϊ_____��
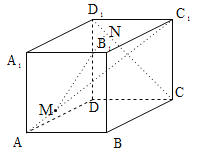
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪˫����![]() ��������ֱ�Ϊ
��������ֱ�Ϊ![]() ��
��![]() Ϊ˫���ߵ�һ�����㣬
Ϊ˫���ߵ�һ�����㣬![]() Ϊ�����һ���˵㣬�����߶�
Ϊ�����һ���˵㣬�����߶�![]() �ϣ������˵㣩��������
�ϣ������˵㣩��������![]() ��ʹ��
��ʹ��![]() ����˫���ߵĽ�����б��
����˫���ߵĽ�����б��![]() ��ƽ����ȡֵ��Χ�ǣ� ��
��ƽ����ȡֵ��Χ�ǣ� ��
A.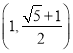 B.
B.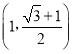 C.
C.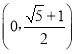 D.
D.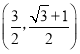
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com