
【题目】已知在平面直角坐标系中的一个椭圆,它的中心在原点,左焦点为 ![]() ,且过点D(2,0).
,且过点D(2,0).
(1)求该椭圆的标准方程;
(2)设点 ![]() ,若P是椭圆上的动点,求线段PA的中点M的轨迹方程.
,若P是椭圆上的动点,求线段PA的中点M的轨迹方程.
【答案】
(1)解:由题意知椭圆的焦点在x轴上,设椭圆的标准方程是 ![]()
∵椭圆经过点D(2,0),左焦点为 ![]() ,
,
∴a=2, ![]() ,可得b=
,可得b= ![]() =1
=1
因此,椭圆的标准方程为 ![]()
(2)解:设点P的坐标是(x0,y0),线段PA的中点为M(x,y),
由根据中点坐标公式,可得 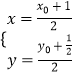 ,整理得
,整理得 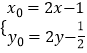 ,
,
∵点P(x0,y0)在椭圆上,
∴可得 ![]() ,化简整理得
,化简整理得 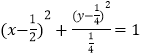 ,
,
由此可得线段PA中点M的轨迹方程是 ![]()
【解析】(1)设椭圆方程为 ![]() ,根据题意可得a=2且c=
,根据题意可得a=2且c= ![]() ,从而b=
,从而b= ![]() =1,得到椭圆的标准方程;(2)设点P(x0 , y0),线段PA的中点为M(x,y),根据中点坐标公式将x0、y0表示成关于x、y的式子,将P(x0 , y0)关于x、y的坐标形式代入已知椭圆的方程,化简整理即可得到线段PA的中点M的轨迹方程.
=1,得到椭圆的标准方程;(2)设点P(x0 , y0),线段PA的中点为M(x,y),根据中点坐标公式将x0、y0表示成关于x、y的式子,将P(x0 , y0)关于x、y的坐标形式代入已知椭圆的方程,化简整理即可得到线段PA的中点M的轨迹方程.
【考点精析】本题主要考查了椭圆的标准方程的相关知识点,需要掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知双曲线的中心在原点,焦点F1 , F2在坐标轴上,离心率为 ![]() ,且过点(4,﹣
,且过点(4,﹣ ![]() ),点M(3,m)在双曲线上.
),点M(3,m)在双曲线上.
(1)求双曲线方程;
(2)求证:MF1⊥MF2;
(3)求△F1MF2的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=f(x)定义域是D,若对任意x1 , x2∈D,当x1<x2时,都有f(x1)≤f(x2),则称函数f(x)在D上为非减函数,设函数y=f(x)在[0,1]上为非减函数,满足条件:①f(0)=0;②f( ![]() )=
)= ![]() f(x);③f(1﹣x)=1﹣f(x);则f(
f(x);③f(1﹣x)=1﹣f(x);则f( ![]() )+f(
)+f( ![]() )= .
)= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆 ![]() 的离心率为
的离心率为 ![]() ,右焦点到直线
,右焦点到直线 ![]() 的距离为
的距离为 ![]() ,过M(0,﹣1)的直线l交椭圆于A,B两点.
,过M(0,﹣1)的直线l交椭圆于A,B两点.
(1)求椭圆的方程;
(2)若直线l交x轴于N, ![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() 的左、右焦点分别为F1、F2 , P为C的右支上一点,且|PF2|=|F1F2|,则
的左、右焦点分别为F1、F2 , P为C的右支上一点,且|PF2|=|F1F2|,则 ![]() 等于( )
等于( )
A.24
B.48
C.50
D.56
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在[1,+∞)的函数,对任意正实数x,f(3x)=3f(x),且f(x)=1﹣|x﹣2|,1≤x≤3,则使得f(x)=f(2015)的最小实数x为( )
A.172
B.415
C.557
D.89
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】二次函数f(x)满足f(x+1)﹣f(x)=2x,且f(0)=1.
(1)求f(x)的解析式;
(2)在区间[﹣1,1]上,y=f(x)的图象恒在y=2x+m的图象上方,试确定实数m的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】本公司计划2009年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元,甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司事来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,PA=AD=AB=2BC,M,N分别为PC,PB的中点. (Ⅰ)求证:PB⊥DM;
(Ⅱ)求CD与平面ADMN所成的角的正弦值.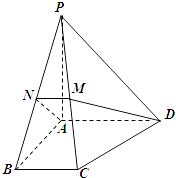
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com