
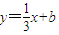 ,且轨迹E上存在不同两点C、D关于直线l对称.
,且轨迹E上存在不同两点C、D关于直线l对称.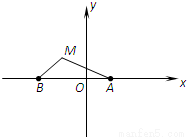
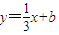 ;所以
;所以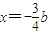 ,
, .又直线CD的方程为
.又直线CD的方程为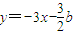 .将直线的方程代入(1)的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用到角公式即可求得b值,从而解决问题.
.将直线的方程代入(1)的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用到角公式即可求得b值,从而解决问题. ,
,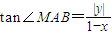 .
. 由∠MBA=2∠MAB(∠MAB≠0),得
由∠MBA=2∠MAB(∠MAB≠0),得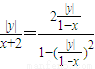 ,
,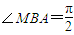 时也满足).
时也满足).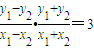 ,即y=-x.
,即y=-x.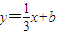 ;所以
;所以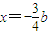 ,
,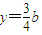 .
.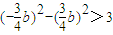 及
及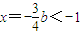 得,
得,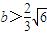 .
. ,即
,即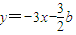 .
.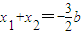 ,
, ,
,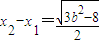 .
.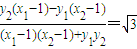
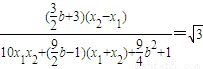 ,即
,即 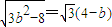 ;解得
;解得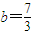 .
.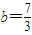 .
.

 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
| 5π |
| 6 |
| OC |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| |TA| |
| |TB| |
| 1 |
| 2 |
| OP |
| OQ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com