练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    (1)已知＝cosα＋isinα，＝cosβ＋isinβ且．求的值；

    (2)求使成立的最小正整数n．

    答案：
    解析：

    　　解 (1)方法1 由已知得cosα＋cosβ＝，sinα＋sinβ＝．∴2sin，．两式相除得，从而cos(α＋β)＝－，sin(α＋β)＝，∴＝cos(α＋β)＋isin(α＋β)＝．

    　　方法2 ∵．∵，即

    　　(2)左式＝

    　　

    　　右式＝

    　　∴，n＝24k－6，k∈N．所以最小正整数n＝18．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：101网校同步练习　高一数学　人教社(新课标B　2004年初审通过) 人教实验版 题型：044

    已知＝(cosα，sinα)，＝(cosβ，sinβ)，0＜α＜β＜π．

    (1)求的值；

    (2)求证：与互相垂直．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本小题满分12分）已知＝(cos＋sin，－sin)，＝(cos－sin，2cos).

     (1)设f(x)＝·，求f(x)的最小正周期和单调递减区间；

    (2)设有不相等的两个实数x1，x2∈，且f(x1)＝f(x2)＝1，求x1＋x2的值.

    查看答案和解析>>

    科目：高中数学 来源：2014届河北衡水中学高一第二学期期末文科数学试卷（解析版） 题型：解答题

    （本小题满分12分）

    已知＝(cos＋sin，－sin)，＝(cos－sin，2cos).

    (1)设f(x)＝·，求f(x)的最小正周期和单调递减区间；

    (2)设有不相等的两个实数x1，x2∈，且f(x1)＝f(x2)＝1，求x1＋x2的值.

     

    查看答案和解析>>

    科目：高中数学 来源：2013届湖北长阳自治县第一中学高二下学期期中理科数学试卷（解析版） 题型：解答题

    已知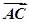＝(cos＋sin，－sin)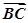，＝(cos－sin，2cos).

    (1)设f(x)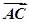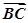＝·，求f(x)的最小正周期和单调递减区间；

    (2)设有不相等的两个实数x1，x2∈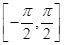，且f(x1)＝f(x2)＝1，求x1＋x2的值.

     

    查看答案和解析>>

    同步练习册答案