
分析 (1)设公比为q(q>0),由a5=2a3+a4,且S5=62,得到关于a1,q方程组,解得即可,
(2)根据数列求和公式,以及裂项求和,和放缩法即可证明
解答 解:(1)设公比为q(q>0),由a5=2a3+a4,且S5=62,
得,$\left\{\begin{array}{l}{{a}_{1}{q}^{4}=2{a}_{1}{q}^{2}+{a}_{1}{q}^{3}}\\{\frac{{a}_{1}(1-{q}^{5})}{1-q}=62}\end{array}\right.$
解得a1=2,q=2,
∴an=2n,
(2)由(1)可知an=2n+1,Sn=$\frac{2(1-{2}^{n})}{1-2}$=2(2n-1),Sn+1=2(2n+1-1),
∴bn=$\frac{{a}_{n+1}}{{S}_{n}{S}_{n+1}}$=$\frac{{2}^{n+1}}{2×({2}^{n}-1)×2×({2}^{n+1}-1)}$=$\frac{1}{2}$($\frac{1}{{2}^{n}-1}$-$\frac{1}{{2}^{n+1}-1}$),
∴Tn=$\frac{1}{2}$[($\frac{1}{{2}^{1}-1}$-$\frac{1}{{2}^{2}-1}$)+($\frac{1}{{2}^{2}-1}$-$\frac{1}{{2}^{3}-1}$)+…+($\frac{1}{{2}^{n}-1}$-$\frac{1}{{2}^{n+1}-1}$)]=$\frac{1}{2}$(1-$\frac{1}{{2}^{n+1}-1}$),
∵n+1≥2,
∴$\frac{1}{{2}^{n+1}-1}$≤$\frac{1}{3}$,
∴$\frac{1}{2}$(1-$\frac{1}{{2}^{n+1}}$)≥$\frac{1}{3}$,且$\frac{1}{2}$(1-$\frac{1}{{2}^{n+1}-1}$)<$\frac{1}{2}$,
∴$\frac{1}{3}$≤Tn<$\frac{1}{2}$.
点评 本题考查了等比数列的通项公式和求和公式,以及裂项求和和放缩法,属于中档题


 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-∞,-\frac{3}{2}})$ | B. | $({-∞,-\frac{3}{4}})$ | C. | $({-\frac{3}{4},+∞})$ | D. | $({-\frac{3}{2},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | n2 | B. | n(n+1) | C. | $\frac{n(n+1)}{2}$ | D. | (n+1)(n+2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{3}{13}$ | D. | $\frac{2}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
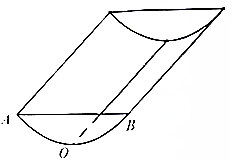 某小区内有一条形状如图的沟渠,沟沿是两条平行线段,沟渠宽AB为20厘米,沟渠的直截面ABO为一段抛物线,抛物线顶点为O,对称轴与地面垂直,沟渠深20厘米,沟渠中水深10厘米.
某小区内有一条形状如图的沟渠,沟沿是两条平行线段,沟渠宽AB为20厘米,沟渠的直截面ABO为一段抛物线,抛物线顶点为O,对称轴与地面垂直,沟渠深20厘米,沟渠中水深10厘米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com