
【题目】某地区实施“光盘行动”以后,某自助啤酒吧也制定了自己的行动计划,进店的每一位客人需预交![]() 元,啤酒根据需要自己用量杯量取,结账时,根据每桌剩余酒量,按一定倍率收费(如下表),每桌剩余酒量不足
元,啤酒根据需要自己用量杯量取,结账时,根据每桌剩余酒量,按一定倍率收费(如下表),每桌剩余酒量不足![]() 升的,按
升的,按![]() 升计算(如剩余
升计算(如剩余![]() 升,记为剩余
升,记为剩余![]() 升).例如:结账时,某桌剩余酒量恰好为
升).例如:结账时,某桌剩余酒量恰好为![]() 升,则该桌的每位客人还应付
升,则该桌的每位客人还应付![]() 元.统计表明饮酒量与人数有很强的线性相关关系,下面是随机采集的
元.统计表明饮酒量与人数有很强的线性相关关系,下面是随机采集的![]() 组数据
组数据![]() (其中
(其中![]() 表示饮酒人数,
表示饮酒人数,![]() (升)表示饮酒量):
(升)表示饮酒量):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
剩余酒量(单位:升) |
|
|
|
|
|
结账时的倍率 |
|
|
|
|
|
(1)求由这![]() 组数据得到的
组数据得到的![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)小王约了![]() 位朋友坐在一桌饮酒,小王及朋友用量杯共量取了
位朋友坐在一桌饮酒,小王及朋友用量杯共量取了![]() 升啤酒,这时,酒吧服务生对小王说,根据他的经验,小王和朋友量取的啤酒可能喝不完,可以考虑再邀请
升啤酒,这时,酒吧服务生对小王说,根据他的经验,小王和朋友量取的啤酒可能喝不完,可以考虑再邀请![]() 位或
位或![]() 位朋友一起来饮酒,会更划算.试向小王是否该接受服务生的建议?
位朋友一起来饮酒,会更划算.试向小王是否该接受服务生的建议?
参考数据:回归直线的方程是![]() ,其中
,其中 ,
,![]() .
.
科目:高中数学 来源: 题型:
【题目】众所周知的“太极图”,其形状如对称的阴阳两鱼互抱在一起,因而也被称为“阴阳鱼太极图”.如图是放在平面直角坐标系中的“太极图”,整个图形是一个圆形,其中黑色阴影区域在![]() 轴右侧部分的边界为一个半圆.给出以下命题:①在太极图中随机取一点,此点取自黑色阴影部分的概率是
轴右侧部分的边界为一个半圆.给出以下命题:①在太极图中随机取一点,此点取自黑色阴影部分的概率是![]() ;②当
;②当![]() 时,直线
时,直线![]() 与黑色阴影部分有公共点;③当
与黑色阴影部分有公共点;③当![]() 时,直线
时,直线![]() 与黑色阴影部分有两个公共点.其中所有正确结论的序号是( )
与黑色阴影部分有两个公共点.其中所有正确结论的序号是( )
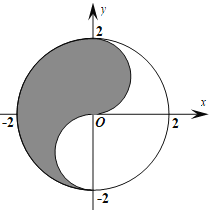
A.①B.①②C.①③D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,定义![]() 为两点A
为两点A![]() B
B![]() 的“切比雪夫距离”,又设点P及
的“切比雪夫距离”,又设点P及![]() 上任意一点Q,称
上任意一点Q,称![]() 的最小值为点P到直线
的最小值为点P到直线![]() 的“切比雪夫距离”,记作
的“切比雪夫距离”,记作![]() ,给出下列三个命题:
,给出下列三个命题:
①对任意三点A、B、C,都有![]()
②已知点P(2,1)和直线![]() ,则
,则![]()
③定点![]() 动点P
动点P![]() 满足
满足![]() 则点P的轨迹与直线
则点P的轨迹与直线![]() (
(![]() 为常数)有且仅有2个公共点.
为常数)有且仅有2个公共点.
其中真命题的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱柱![]() 中,底面
中,底面![]() 是正三角形,侧棱
是正三角形,侧棱![]() 底面
底面![]() .D,E分别是边BC,AC的中点,线段
.D,E分别是边BC,AC的中点,线段![]() 与
与![]() 交于点G,且
交于点G,且![]() ,
,![]() .
.

(1)求证:![]() ∥平面
∥平面![]() ;
;
(2)求证:![]() ⊥平面
⊥平面![]() ;
;
(3)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为矩形,平面
为矩形,平面![]()
![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 中点.
中点.

(Ⅰ)求证:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]()
![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于集合![]() ,
,![]() ,
,![]() ,
,![]() .集合
.集合![]() 中的元素个数记为
中的元素个数记为![]() .规定:若集合
.规定:若集合![]() 满足
满足![]() ,则称集合
,则称集合![]() 具有性质
具有性质![]() .
.
(I)已知集合![]() ,
,![]() ,写出
,写出![]() ,
,![]() 的值;
的值;
(II)已知集合![]() ,
,![]() 为等比数列,
为等比数列,![]() ,且公比为
,且公比为![]() ,证明:
,证明:![]() 具有性质
具有性质![]() ;
;
(III)已知![]() 均有性质
均有性质![]() ,且
,且![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题:①设![]() ,则
,则![]() 是
是![]() 的充要条件;②已知命题
的充要条件;②已知命题![]() 、
、![]() 、
、![]() 满足“
满足“![]() 或
或![]() ”真,“
”真,“![]() 或
或![]() ”也真,则“
”也真,则“![]() 或
或![]() ”假;③若
”假;③若![]() ,则使得
,则使得![]() 恒成立的
恒成立的![]() 的取值范围为{
的取值范围为{![]() 或
或![]() };④将边长为
};④将边长为![]() 的正方形
的正方形![]() 沿对角线
沿对角线![]() 折起,使得
折起,使得![]() ,则三棱锥
,则三棱锥![]() 的体积为
的体积为![]() .其中真命题的序号为________.
.其中真命题的序号为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣a)2+(y﹣2)2=4(a>0)及直线l:x﹣y+3=0.当直线l被圆C截得的弦长为![]() 时,求
时,求
(Ⅰ)a的值;
(Ⅱ)求过点(3,5)并与圆C相切的切线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某隧道设计为双向四车道,车道总宽22米,要求通行车辆限高4.5米,隧道全长2.5千米,隧道的拱线近似地看成半个椭圆形状.

(1)若最大拱高h为6米,则隧道设计的拱宽l是多少?
(2)若最大拱高h不小于6米,则应如何设计拱高h和拱宽l,才能使半个椭圆形隧道的土方工程量最最小?(半个椭圆的面积公式为![]() ,柱体体积为:底面积乘以高.本题结果精确到0.1米)
,柱体体积为:底面积乘以高.本题结果精确到0.1米)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com