
| A. | 2 | B. | $\sqrt{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\sqrt{5}$ |
分析 设A(x1,y1),B((x2,y2),则x1+x2=-$\frac{2}{3}$.
由$\left\{\begin{array}{l}{y=x+1}\\{m{x}^{2}+n{y}^{2}=1}\end{array}\right.$得(m+n)x2+2nx+n-1=0⇒x1+x2=$\frac{-2n}{m+n}=-\frac{2}{3}$⇒m=2n即可.
解答 解:设A(x1,y1),B((x2,y2),则x1+x2=-$\frac{2}{3}$.
由$\left\{\begin{array}{l}{y=x+1}\\{m{x}^{2}+n{y}^{2}=1}\end{array}\right.$得(m+n)x2+2nx+n-1=0⇒x1+x2=$\frac{-2n}{m+n}=-\frac{2}{3}$⇒m=2n
双曲线$\frac{y^2}{m^2}-\frac{x^2}{n^2}$=1的离心率e,e2=$1+\frac{{n}^{2}}{{m}^{2}}=\frac{5}{4}$⇒e=$\frac{\sqrt{5}}{2}$.
故选:C
点评 本题考查了直线与椭圆的位置关系,及双曲线离心率,属于中档题.


科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{3}\overrightarrow{AB}-\frac{2}{3}\overrightarrow{AD}$ | B. | $\frac{2}{3}\overrightarrow{AB}-\frac{1}{3}\overrightarrow{AD}$ | C. | $-\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$ | D. | $-\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AD}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在三角形中,若A>B,则sinA>sinB | |
| B. | 若等比数列的前n项和Sn=2n+k,则必有k=-1 | |
| C. | A,B为两个定点,k为非零常数,|$\overrightarrow{PA}|-|\overrightarrow{PB}$|=k,则动点P的轨迹为双曲线 | |
| D. | 曲线$\frac{x^2}{16}-\frac{y^2}{9}$=1与曲线$\frac{x^2}{35-λ}+\frac{y^2}{10-λ}$=1(λ<10)有相同的焦点 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
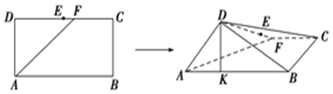 如图,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点,现将△AFD沿AF折起,使平面ABD⊥平面ABCF.在平面ABD内过点D作DK⊥AB,K为垂足,设AK=t,则t的取值范围是( )
如图,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点,现将△AFD沿AF折起,使平面ABD⊥平面ABCF.在平面ABD内过点D作DK⊥AB,K为垂足,设AK=t,则t的取值范围是( )| A. | ($\frac{1}{2}$,2) | B. | ($\frac{1}{2}$,1) | C. | ($\frac{\sqrt{3}}{2}$,2) | D. | ($\frac{\sqrt{3}}{2}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
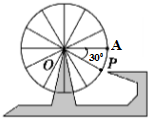 如图所示,一个半径为10m的摩天轮,轮子的底部在地面上2m处,如果此摩天轮按逆时针方向转动,每30s转一圈,且当摩天轮上某人经过点P处(∠POA=30°)时开始计时.
如图所示,一个半径为10m的摩天轮,轮子的底部在地面上2m处,如果此摩天轮按逆时针方向转动,每30s转一圈,且当摩天轮上某人经过点P处(∠POA=30°)时开始计时.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com