
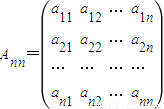 ,其中对任意的1≤i≤n,1≤j≤n,当i能整除j时,aij=1;当i不能整除j时,aij=0.设
,其中对任意的1≤i≤n,1≤j≤n,当i能整除j时,aij=1;当i不能整除j时,aij=0.设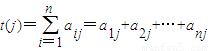 .
.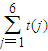 ;
;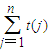 =
=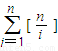 ;
;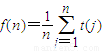 ,
,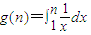 ,求证:g(n)-1<f(n)<g(n)+1.
,求证:g(n)-1<f(n)<g(n)+1.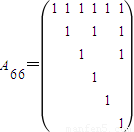 .
. 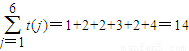 .
.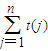 是数阵Ann所有数的和.而数阵Ann所有数的和也可以考虑按行相加.对任意的1≤i≤n,不超过n的倍数有1i,2i,…,
是数阵Ann所有数的和.而数阵Ann所有数的和也可以考虑按行相加.对任意的1≤i≤n,不超过n的倍数有1i,2i,…,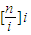 .因此数阵Ann的第i行中有
.因此数阵Ann的第i行中有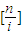 个1,其余是0,即第i行的和为
个1,其余是0,即第i行的和为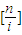 .从而得到结果.
.从而得到结果.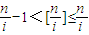 ,所以
,所以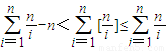 .所以
.所以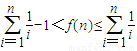 .再考查定积分
.再考查定积分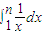 ,根据曲边梯形的面积的计算即可证得结论.
,根据曲边梯形的面积的计算即可证得结论.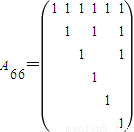 .
. 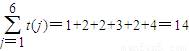 .
. 是数阵Ann所有数的和.
是数阵Ann所有数的和.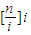 .
.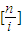 个1,其余是0,即第i行的和为
个1,其余是0,即第i行的和为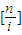 .
.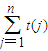 =
=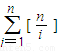 .
.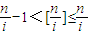 ,
,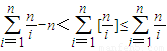 .所以
.所以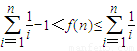 .
.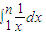 ,将区间[1,n]分成n-1等分,则
,将区间[1,n]分成n-1等分,则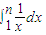 的不足近似值为
的不足近似值为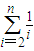 ,
,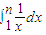 的过剩近似值为
的过剩近似值为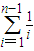 . 所以
. 所以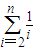
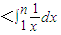
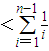 .
.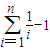 <g(n)
<g(n)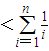 .所以g(n)-1<
.所以g(n)-1<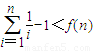
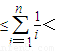 g(n)+1.
g(n)+1.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| x |
| 3 |
| 2 |
| 1 |
| 2n+1 |
| a1 |
| a2 |
| a2 |
| a3 |
| an |
| an+1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| S(m+1)n | Smn |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| n |
 |
| i=1 |
| 6 |
 |
| j=1 |
| n |
 |
| j=1 |
| n |
 |
| i=1 |
| n |
| i |
| 1 |
| n |
| n |
 |
| j=1 |
| ∫ | n 1 |
| 1 |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| n |
 |
| i=1 |
| n |
 |
| j=1 |
| n |
 |
| i=1 |
| n |
| i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com