
【题目】在平面直角坐标系xOy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcosθ+ρsinθ=1,曲线C的极坐标方程为ρsin2θ=8cosθ.
(1)求直线l与曲线C的直角坐标方程;
(2)设点M(0,1),直线l与曲线C交于不同的两点P,Q,求|MP|+|MQ|的值.
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() (其中e为自然对数的底数,m、n为常数),函数
(其中e为自然对数的底数,m、n为常数),函数![]() 定义为:对每一个给定的实数x,
定义为:对每一个给定的实数x,
(1)当m、n满足什么条件时,![]() 对所有的实数x恒成立;
对所有的实数x恒成立;
(2)设a、b是两个实数,满足![]() 且m,
且m,![]() 当
当![]() 时,求函数
时,求函数![]() 在区间
在区间![]() 的上的单调增区间的长度之和(用含a、b的式子表示)(闭区间
的上的单调增区间的长度之和(用含a、b的式子表示)(闭区间![]() 的长度定义为
的长度定义为![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面ABCD为直角梯形,AD//BC,且![]() ,BC⊥DC,∠BAD=60°,平面PAD⊥底面ABCD,E为AD的中点,△PAD为等边三角形,M是棱PC上的一点,设
,BC⊥DC,∠BAD=60°,平面PAD⊥底面ABCD,E为AD的中点,△PAD为等边三角形,M是棱PC上的一点,设![]() (M与C不重合).
(M与C不重合).
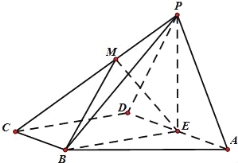
(1)求证:CD⊥DP;
(2)若PA∥平面BME,求k的值;
(3)若二面角M﹣BE﹣A的平面角为150°,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的标准方程为
的标准方程为![]() ,该椭圆经过点
,该椭圆经过点![]() ,且离心率为
,且离心率为![]() .
.
(1)求椭圆的标准方程;
(2)过椭圆![]() 长轴上一点
长轴上一点![]() 作两条互相垂直的弦
作两条互相垂直的弦![]() .若弦
.若弦![]() 的中点分别为
的中点分别为![]() ,证明:直线
,证明:直线![]() 恒过定点.
恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位共有10名员工,他们某年的收入如下表:
员工编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
年薪(万元) | 4 | 4.5 | 6 | 5 | 6.5 | 7.5 | 8 | 8.5 | 9 | 51 |
(1)求该单位员工当年年薪的平均值和中位数;
(2)已知员工年薪收入与工作年限成正相关关系,某员工工作第一年至第四年的年薪分别为4万元、5.5万元、6万元、8.5万元,预测该员工第六年的年薪为多少?
附:线性回归方程![]() 中系数计算公式分别为:
中系数计算公式分别为: ,
,![]() ,其中
,其中![]() 、
、![]() 为样本均值.
为样本均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆C:![]() (a>b>0)过点
(a>b>0)过点![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆C的方程;
(2)若斜率为![]() 的直线l与椭圆C交于A,B两点,试探究
的直线l与椭圆C交于A,B两点,试探究![]() 是否为定值?若是定值,则求出此定值;若不是定值,请说明理由.
是否为定值?若是定值,则求出此定值;若不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先阅读下列不等式的证法,再解决后面的问题:
已知![]() ,
,![]() ,求证:
,求证:![]() .
.
证明:构造函数![]() ,
,
即![]()
![]() .
.
因为对一切![]() ,恒有
,恒有![]() ,
,
所以![]() ,从而得
,从而得![]() .
.
(1)若![]() ,
,![]() ,请写出上述结论的推广式;
,请写出上述结论的推广式;
(2)参考上述证法,对你推广的结论加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com