
【题目】下列判断正确的是( )
A.“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
B.函数![]() 的最小值为2
的最小值为2
C.当![]() 时,命题“若
时,命题“若![]() ,则
,则![]() ”为真命题
”为真命题
D.命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
科目:高中数学 来源: 题型:
【题目】交大设计学院植物园准备用一块边长为4百米的等边ΔABC田地(如图)建立芳香植物生长区、植物精油提炼处与植物精油体验点.田地内拟建笔直小路MN、AP,其中M、N分别为AC、BC的中点,点P在CN上.规划在小路MN和AP的交点O(O与M、N不重合)处设立植物精油体验点,图中阴影部分为植物精油提炼处,空白部分为芳香植物生长区,A、N为出入口(小路宽度不计).为节约资金,小路MO段与OP段建便道,供芳香植物培育之用,费用忽略不计,为车辆安全出入,小路AO段的建造费用为每百米4万元,小路ON段的建造费用为每百米3万元.
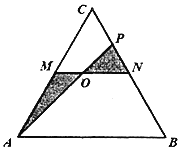
(1)若拟建的小路AO段长为![]() 百米,求小路ON段的建造费用;
百米,求小路ON段的建造费用;
(2)设∠BAP=![]() ,求
,求![]() 的值,使得小路AO段与ON段的建造总费用最小,并求岀最小建造总费用(精确到元).
的值,使得小路AO段与ON段的建造总费用最小,并求岀最小建造总费用(精确到元).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为D的函数y=f(x),如果存在区间[m,n]![]() D,同时满足:
D,同时满足:
①f(x)在[m,n]内是单调函数;
②当定义域是[m,n]时,f(x)的值域也是[m,n].则称[m,n]是该函数的“和谐区间”.
(1)证明:[0,1]是函数y=f(x)=x2的一个“和谐区间”.
(2)求证:函数![]() 不存在“和谐区间”.
不存在“和谐区间”.
(3)已知:函数![]() (a∈R,a≠0)有“和谐区间”[m,n],当a变化时,求出n﹣m的最大值.
(a∈R,a≠0)有“和谐区间”[m,n],当a变化时,求出n﹣m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() (m,n为常数),在
(m,n为常数),在![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅰ)求![]() 的解析式并写出定义域;
的解析式并写出定义域;
(Ⅱ)若![]() ,使得对
,使得对![]() 上恒有
上恒有![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)若![]() 有两个不同的零点
有两个不同的零点![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,过
,过![]() 作
作![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 于点
于点![]() (点
(点![]() 在
在![]() 轴上方),斜率为
轴上方),斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,且
,且![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)设椭圆![]() 的离心率为
的离心率为![]() ,当点
,当点![]() 为椭圆
为椭圆![]() 的右顶点时,
的右顶点时,![]() 的坐标为
的坐标为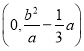 ,求
,求![]() 的值.
的值.
(2)若椭圆![]() 的方程为
的方程为![]() ,且
,且![]() ,是否存
,是否存![]() 在使得
在使得![]() 成立?如果存在,求出
成立?如果存在,求出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com