
【题目】设min{m,n}表示m,n二者中较小的一个,已知函数f(x)=x2+8x+14,g(x)=![]() (x>0),若x1∈[-5,a](a≥-4),x2∈(0,+∞),使得f(x1)=g(x2)成立,则a的最大值为
(x>0),若x1∈[-5,a](a≥-4),x2∈(0,+∞),使得f(x1)=g(x2)成立,则a的最大值为
A.-4B.-3C.-2D.0
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:
【题目】某赛季甲、乙两位运动员每场比赛得分的茎叶图如图所示.
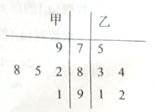
(1)从甲、乙两人的这5次成绩中各随机抽取一个,求甲的成绩比乙的成绩高的概率;
(2)试用统计学中的平均数、方差知识对甲、乙两位运动员的测试成绩进行分析.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,经统计,频率分布直方图如图所示:
(单位:克)中,经统计,频率分布直方图如图所示:
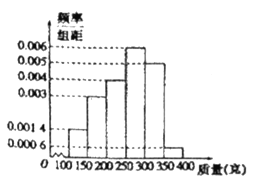
(1)估计这组数据的平均数(同一组中的数据以这组数据所在区间中点的值作代表);
(2)现按分层抽样从质量为![]() ,
,![]() 的芒果中随机抽取5个,再从这5个中随机抽取2个,求这2个芒果都来自同一个质量区间的概率;
的芒果中随机抽取5个,再从这5个中随机抽取2个,求这2个芒果都来自同一个质量区间的概率;
(3)某经销商来收购芒果,同一组中的数据以这组数据所在区间中点的值作代表,用样本估计总体,该种植园中还未摘下的芒果大约还有1000个,经销商提出以下两种收购方案:
方案①:所有芒果以9元/千克收购
方案②:对质量低于250克的芒果以2元/个收购,对质量高于或等于250克的芒果以3元/个收购.通过计算确定种植园选择哪种方案获利更多.
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 分别是椭圈
分别是椭圈![]() 的左、右焦点,椭圆
的左、右焦点,椭圆![]() 的焦点
的焦点![]() 到双曲线
到双曲线![]() 渐近线的距离为
渐近线的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,以线段
两点,以线段![]() 为直径的圆经过点
为直径的圆经过点![]() ,且原点
,且原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机询问100名性别不同的大学生是否爱好踢毽子,得到如下的列联表:

随机变量![]() 经计算,统计量K2的观测值k0≈4.762,参照附表,得到的正确结论是( )
经计算,统计量K2的观测值k0≈4.762,参照附表,得到的正确结论是( )
A. 在犯错误的概率不超过5%的前提下,认为“爱好该项运动与性别有关”
B. 在犯错误的概率不超过5%的前提下,认为“爱好该项运动与性别无关”
C. 有97.5%以上的把握认为“爱好该项运动与性别有关”
D. 有97.5%以上的把握认为“爱好该项运动与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 1(a>b>0)的右顶点为A(2,0),离心率为
1(a>b>0)的右顶点为A(2,0),离心率为![]() .
.
(1)求椭圆C的方程;
(2)设过点P(0,﹣2)的直线l与椭圆C相交于M,N两点,当△OMN的面积最大时(O为坐标原点),求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】.
为了解某校高三学生质检数学成绩分布,从该校参加质检的学生数学成绩中抽取一个样本,并分成5组,绘成如图所示的频率分布直方图.若第一组至第五组数据的频率之比为![]() ,最后一组数据的频数是6.
,最后一组数据的频数是6.
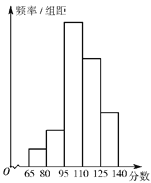
(Ⅰ)估计该校高三学生质检数学成绩在125~140分之间的概率,并求出样本容量;
(Ⅱ)从样本中成绩在65~95分之间的学生中任选两人,求至少有一人成绩在65~80分之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图几何体是圆锥的一部分,它是Rt△ABC(及其内部)以一条直角边AB所在直线为旋转轴旋转150°得到的,AB=BC=2,P是弧![]() 上一点,且EB⊥AP.
上一点,且EB⊥AP.
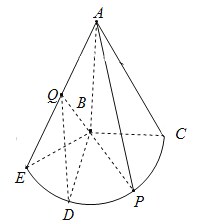
(1)求∠CBP的大小;
(2)若Q为AE的中点,D为弧![]() 的中点,求二面角Q﹣BD﹣P的余弦值;
的中点,求二面角Q﹣BD﹣P的余弦值;
(3)直线AC上是否存在一点M,使得B、D、M、Q四点共面?若存在,请说明点M的位置;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com