
【题目】某中学对高二甲、乙两个同类班级进行“加强‘语文阅读理解’训练对提高‘数学应用题’得分率有帮助”的试验,其中甲班为试验班(加强语文阅读理解训练),乙班为对比班(常规教学,无额外训练),在试验前的测试中,甲、乙两班学生在数学应用题上的得分率基本一致,试验结束后,统计几次数学应用题测试的平均成绩(均取整数)如下表所示:
60分及以下 | 61~70分 | 71~80分 | 81~90分 | 91~100分 | |
甲班(人数) | 3 | 6 | 12 | 15 | 9 |
乙班(人数) | 4 | 7 | 16 | 12 | 6 |
现规定平均成绩在80分以上(不含80分)的为优秀.
(1)由以上统计数据填写![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“加强‘语文阅读理解’训练对提高‘数学应用题’得分率”有帮助;
的把握认为“加强‘语文阅读理解’训练对提高‘数学应用题’得分率”有帮助;
(2)对甲乙两班60分及以下的同学进行定期辅导,一个月后从中抽取3人课堂检测,![]() 表示抽取到的甲班学生人数,求
表示抽取到的甲班学生人数,求![]() 及至少抽到甲班1名同学的概率.
及至少抽到甲班1名同学的概率.
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:
【题目】对于函数![]() 和
和![]() ,若存在区间
,若存在区间![]() ,使
,使![]() 在区间
在区间![]() 上恒成立,则称区间
上恒成立,则称区间![]() 是函数
是函数![]() 和
和![]() 的“公共邻域”.设函数
的“公共邻域”.设函数![]() 的反函数为
的反函数为![]() ,函数
,函数![]() 的图像与函数
的图像与函数![]() 的图像关于点
的图像关于点![]() 对称.
对称.
(1)求函数![]() 和
和![]() 的解析式;
的解析式;
(2)若![]() ,求函数
,求函数![]() 的定义域;
的定义域;
(3)是否存在实数![]() ,使得区间
,使得区间![]() 是
是![]() 和
和![]() 的“公共邻域”,若存在,求出
的“公共邻域”,若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)求函数f(x)的定义域,判断并证明函数f(x)的奇偶性;
(Ⅱ)是否存在这样的实数k,使f(k-x2)+f(2k-x4)≥0对一切![]() 恒成立,若存在,试求出k的取值集合;若不存在,请说明理由.
恒成立,若存在,试求出k的取值集合;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新个税法于2019年1月1日进行实施.为了调查国企员工对新个税法的满意程度,研究人员在![]() 地各个国企中随机抽取了1000名员工进行调查,并将满意程度以分数的形式统计成如下的频率分布直方图,其中
地各个国企中随机抽取了1000名员工进行调查,并将满意程度以分数的形式统计成如下的频率分布直方图,其中![]() .
.
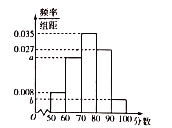
(1)求![]() 的值并估计被调查的员工的满意程度的中位数;(计算结果保留两位小数)
的值并估计被调查的员工的满意程度的中位数;(计算结果保留两位小数)
(2)若按照分层抽样从![]() ,
,![]() 中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在
中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分形理论是当今世界十分风靡和活跃的新理论、新学科。其中,把部分与整体以某种方式相似的形体称为分形。分形是一种具有自相似特性的现象,图象或者物理过程。标准的自相似分形是数学上的抽象,迭代生成无限精细的结构。也就是说,在分形中,每一组成部分都在特征上和整体相似,只仅仅是变小了一些而已,谢尔宾斯基三角形就是一种典型的分形,是由波兰数学家谢尔宾斯基在1915年提出的,按照如下规律依次在一个黑色三角形内去掉小三角形则当![]() 时,该黑色三角形内共去掉( )个小三角形
时,该黑色三角形内共去掉( )个小三角形
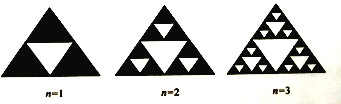
A. 81 B. 121 C. 364 D. 1093
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,双十一购物狂欢节(简称“双11”)活动已成为中国电子商务行业年度盛事,某网络商家为制定2018年“双11”活动营销策略,调查了2017年“双11”活动期间每位网购客户用于网购时间![]() (单位:小时),发现
(单位:小时),发现![]() 近似服从正态分布
近似服从正态分布![]() .
.
(1)求![]() 的估计值;
的估计值;
(2)该商家随机抽取参与2017年“双11”活动的10000名网购客户,这10000名客户在2017年“双11”活动期间,用于网购时间![]() 属于区间
属于区间![]() 的客户数为
的客户数为![]() .该商家计划在2018年“双11”活动前对这
.该商家计划在2018年“双11”活动前对这![]() 名客户发送广告,所发广告的费用为每位客户0.05元.
名客户发送广告,所发广告的费用为每位客户0.05元.
(i)求该商家所发广告总费用的平均估计值;
(ii)求使![]() 取最大值时的整数
取最大值时的整数![]() 的值.
的值.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,
![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com