
【题目】设数列{an}的前n项和为Sn , 且Sn=n2﹣4n﹣5.
(1)求数列{an}的通项公式;
(2)设bn=|an|,数列{bn}的前n项和为Tn , 求Tn .
【答案】
(1)解:∵Sn=n2﹣4n﹣5,
∴当n≥2时,an=Sn﹣Sn﹣1=n2﹣4n﹣5﹣[(n﹣1)2﹣4(n﹣1)﹣5]=2n﹣5,
又当n=1时,a1=﹣8不适合上式,
∴an= ![]()
(2)解:∵bn=|an|,数列{bn}的前n项和为Tn,
当n=1时,b1=|a1|=8,T1=8;
当n=2时,b2=|a2|=1,T2=8+1=9;
∵n≥3时,an=2n﹣5≥1>0,
∴bn=|an|=an=2n﹣5,
∴Tn=8+1+(1+3+…+2n﹣5)=9+ ![]() =(n﹣2)2+9=n2﹣4n+13.
=(n﹣2)2+9=n2﹣4n+13.
综上,Tn= 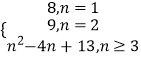
【解析】(1)由Sn=n2﹣4n﹣5,可得当n≥2时,an=Sn﹣Sn﹣1=2n﹣5,再检验当n=1时,a1是否适合上式,即可求得数列{an}的通项公式;(2)由bn=|an|=|2n﹣5|,分n=1、n=2、n≥3三类讨论,分别求得数列{bn}的前n项和Tn , 最后综合起来即可求.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系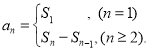 ,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且2asinA=(2b+c)sinB+(2c+b)sinC.
(1)求A的大小;
(2)求sinB+sinC的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象在
的图象在![]() 处的切线方程为
处的切线方程为![]() ,其中
,其中![]() 是自然对数的底数.
是自然对数的底数.
(1)若对任意的![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(2)若函数![]() 的两个零点为
的两个零点为![]() ,试判断
,试判断![]() 的正负,并说明理由.
的正负,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B,C为锐角△ABC的内角, ![]() =(sinA,sinBsinC),
=(sinA,sinBsinC), ![]() =(1,﹣2),
=(1,﹣2), ![]() ⊥
⊥ ![]() .
.
(1)tanB,tanBtanC,tanC能否构成等差数列?并证明你的结论;
(2)求tanAtanBtanC的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() ,分数在
,分数在![]() 以上(含
以上(含![]() )的同学获奖. 按文理科用分层抽样的方法抽取
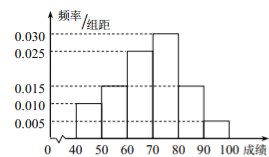
)的同学获奖. 按文理科用分层抽样的方法抽取![]() 人的成绩作为样本,得到成绩的频率分布直方图(见下图).
人的成绩作为样本,得到成绩的频率分布直方图(见下图).
(1)填写下面的![]() 列联表,能否有超过
列联表,能否有超过![]() 的把握认为“获奖与学生的文理科有关”?
的把握认为“获奖与学生的文理科有关”?
(2)将上述调査所得的频率视为概率,现从参赛学生中,任意抽取![]() 名学生,记“获奖”学生人数为
名学生,记“获奖”学生人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
文科生 | 理科生 | 合计 | |
获奖 |
| ||
不获奖 | |||
合计 |
|
附表及公式:
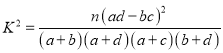 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠CDA=∠BAD=90°,AB=AD=2DC=2 ![]() ,PA=4且E为PB的中点.
,PA=4且E为PB的中点. 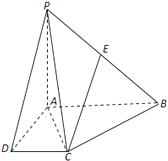
(1)求证:CE∥平面PAD;
(2)求直线CE与平面PAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要得到函数y= ![]() cosx的图象,需将函数y=
cosx的图象,需将函数y= ![]() sin(2x+
sin(2x+ ![]() )的图象上所有的点的变化正确的是( )
)的图象上所有的点的变化正确的是( )
A.横坐标缩短到原来的 ![]() 倍(纵坐标不变),再向左平行移动
倍(纵坐标不变),再向左平行移动 ![]() 个单位长度
个单位长度
B.横坐标缩短到原来的 ![]() 倍(纵坐标不变),再向右平行移动
倍(纵坐标不变),再向右平行移动 ![]() 个单位长度
个单位长度
C.横坐标伸长到原来的2倍(纵坐标不变),再向左平行移动 ![]() 个单位长度
个单位长度
D.横坐标伸长到原来的2倍(纵坐标不变),再向右平行移动 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,an+1+an= ![]() ﹣
﹣ ![]() ,n∈N* .
,n∈N* .
(Ⅰ)求a2 , a3 , a4;
(Ⅱ)猜想数列{an}的通项公式,并用数学归纳法证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com