
分析 由f(1)=2,求出m的值,写出f(x)的解析式;
(1)利用奇偶性的定义判断f(x)定义域上的奇函数;
(2)利用定义证明f(x)在(0,1]上是单调减函数;
(3)同理可证f(x)是[1,+∞)上的单调增函数,
再由单调性的定义转化不等式f(k)>2,从而求出k的取值范围.
解答 解:由f(1)=2,
得$\frac{{1}^{2}+m}{1}$=2,
解得m=1;…(1分)
∴f(x)=$\frac{{x}^{2}+1}{x}$=x+$\frac{1}{x}$;
(1)∵f(x)定义域为(-∞,0)∪(0,+∞),关于原点对称;
且$f(-x)=(-x)+\frac{1}{-x}=-(x+\frac{1}{x})=-f(x)$,
∴f(x)是定义域上的奇函数;…(4分)
(2)f(x)在(0,1]上是单调减函数;
证明:设x1,x2是(0,1]上的任意两个实数,且x1<x2…(5分)
则$f({x_2})-f({x_1})=({x_2}+\frac{1}{x_2})-({x_1}+\frac{1}{x_1})$…(6分)
=$({x_2}-{x_1})+(\frac{1}{x_2}-\frac{1}{x_1})$
=$({x_2}-{x_1})+\frac{{{x_1}-{x_2}}}{{{x_1}{x_2}}}$
=$({x_2}-{x_1})(1-\frac{1}{{{x_1}{x_2}}})$;…(7分)
∵0<x1<x2≤1,
∴${x_2}-{x_1}>0,0<{x_1}{x_2}<1,1-\frac{1}{{{x_1}{x_2}}}<0$;…(8分)
∴f(x2)-f(x1)<0,
∴f(x1)>f(x2);…(9分)
∴f(x)在(0,1]上是单调减函数.…(10分)
(3)同理可证f(x)在[1,+∞)上是单调增函数;…(11分)
由f(k)>2得f(k)>f(1),…(12分)
∴k>1或0<k<1;…(13分)
即所求k的取值范围是(0,1)∪(1,+∞). …(14分
点评 本题考查了函数的奇偶性与单调性的定义与应用问题,是综合性题目.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:解答题
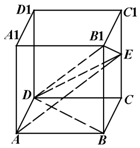 在正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.
在正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
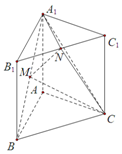 如图,直三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,AA1=2,点M,N分别为A1B和B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,AA1=2,点M,N分别为A1B和B1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
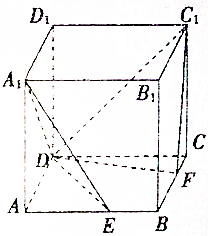 如图所示,ABCD-A1B1C1D1是棱长为6的正方体,E,F分别是棱AB,BC上的动点,且AE=BF.当A1,E,F,C1共面时,平面A1DE与平面C1DF所成锐二面角的余弦值为( )
如图所示,ABCD-A1B1C1D1是棱长为6的正方体,E,F分别是棱AB,BC上的动点,且AE=BF.当A1,E,F,C1共面时,平面A1DE与平面C1DF所成锐二面角的余弦值为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{5}$ | D. | $\frac{2\sqrt{6}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -4 | C. | 6 | D. | -6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com