
已知椭圆 经过点
经过点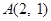 ,离心率为
,离心率为 ,过点
,过点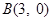 的直线
的直线 与椭圆
与椭圆 交于不同的两点
交于不同的两点 .
.
(1)求椭圆 的方程;
的方程;
(2)求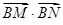 的取值范围.
的取值范围.
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:高中数学 来源: 题型:解答题
已知椭圆的顶点与双曲线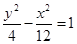 的焦点重合,它们的离心率之和为
的焦点重合,它们的离心率之和为 ,若椭圆的焦点在y轴上.
,若椭圆的焦点在y轴上.
(1)求双曲线的离心率,并写出其渐近线方程;
(2)求椭圆的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆C1: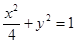 和动圆C2:
和动圆C2: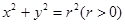 ,直线
,直线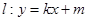 与C1和C2分别有唯一的公共点A和B.
与C1和C2分别有唯一的公共点A和B.
(I)求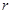 的取值范围;
的取值范围;
(II )求|AB|的最大值,并求此时圆C2的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
直线y=kx+b与曲线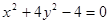 交于A、B两点,记△AOB的面积为S(O是坐标原点).
交于A、B两点,记△AOB的面积为S(O是坐标原点).
(1)求曲线的离心率;
(2)求在k=0,0<b<1的条件下,S的最大值;
(3)当|AB|=2,S=1时,求直线AB的方程.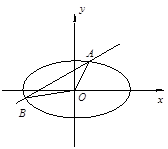
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)如图,椭圆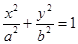 上的点M与椭圆右焦点
上的点M与椭圆右焦点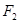 的连线
的连线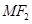 与x轴垂直,且OM(O是坐标原点)与椭圆长轴和短轴端点的连线AB平行.
与x轴垂直,且OM(O是坐标原点)与椭圆长轴和短轴端点的连线AB平行.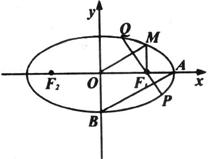
(1)求椭圆的离心率;
(2)过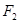 且与AB垂直的直线交椭圆于P、Q,若
且与AB垂直的直线交椭圆于P、Q,若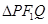 的面积是
的面积是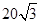 ,求此时椭圆的方程.
,求此时椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
设椭圆C1的离心率为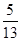 ,焦点在x轴上且长轴长为26,若曲线C2上的点到椭圆C1的两个焦点的距离的差的绝对值等于8,则曲线C2的标准方程为 _____________。
,焦点在x轴上且长轴长为26,若曲线C2上的点到椭圆C1的两个焦点的距离的差的绝对值等于8,则曲线C2的标准方程为 _____________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com