已知{an}是首项为1的等比数列.且a4=8.则数列$\left\{{\frac{1}{a n}}\right\}$的前5项和为( )A．31B．$\frac{31}{16}$C．11D．$\frac{11}{16}$ 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

4．已知{a_n}是首项为1的等比数列，且a₄=8，则数列$\left\{{\frac{1}{a_n}}\right\}$的前5项和为（　　）

A．

B．

$\frac{31}{16}$

C．

D．

$\frac{11}{16}$

分析求出数列的公比，锐角利用等比数列求和公式求解即可．

解答解：{a_n}是首项为1的等比数列，且a₄=8，可得q³=8，可得q=2，
数列$\left\{{\frac{1}{a_n}}\right\}$也是等比数列，公比为：$\frac{1}{2}$，首项为1．
它的前5项和为：$\frac{1-{（\frac{1}{2}）}^{5}}{1-\frac{1}{2}}$=$\frac{31}{16}$．
故选：B．

点评本题考查等比数列求和公式的应用，是基础题．

练习册系列答案

Short Stories for Comprehension妙语短篇系列答案

小夫子卡卡漫游系列答案

深圳市初中学业水平考试系列答案

小升初集结号系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：填空题

14．下列结论：
①若命题p：存在x∈R，tan x=2；命题q：任意x∈R，x²-x+$\frac{1}{2}$＞0．则命题“p且（非q）”是假命题；
②已知直线l₁：ax+3y-1=0，l₂：x+by+1=0，则l₁⊥l₂的充要条件是$\frac{a}{b}$=-3；
③设F₁，F₂是双曲线C：$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1（a＞0，b＞0）的两个焦点，P是C上一点，若|PF₁|+|PF₂|=6a，且△PF₁F₂的最小内角为30°，则C的离心率为$\sqrt{3}$．
④设正实数x，y，z满足x²-3xy+4y²-z=0，则当$\frac{xy}{z}$取得最大值时，$\frac{2}{x}$+$\frac{1}{y}$-$\frac{2}{z}$的最大值为1．
其中正确结论的序号为①③④．（把你认为正确结论的序号都填上）

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

15．函数y=sin2x+cos2x在[0，π]上的单调递减区间为[$\frac{π}{8}$，$\frac{5π}{8}$]．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

12．

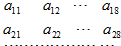（理）64个正数排成8行8列，如图所示：在符号a_ij（1≤i≤8，1≤j≤8）中，i表示该数所在的行数，j表示该数所在的列数．已知每一行都成等差数列，而每一列都成等比数列（且每列公比都相等）．若a₁₁=$\frac{1}{2}$，a₂₄=1，a₃₂=$\frac{1}{4}$．则a₈₁a₈₂…a₈₈…a_ij=j（$\frac{1}{2}$）ⁱ．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

19．下列命题错误的是（　　）

	A．	命题“若x²+y²=0，则x=y=0”的逆否命题为“若x，y中至少有一个不为0则x²+y²≠0”．
	B．	若命题$p：?{x_0}∈R，x_0^2-{x_0}+1≤0$，则?p：?x∈R，x²-x+1＞0．
	C．	△ABC中，sinA＞sinB是A＞B的充要条件．
	D．	?φ∈R，函数f（x）=sin（2x+φ）都不是偶函数．