
【题目】已知椭圆![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() ,
,![]() ,离心率
,离心率![]() ,椭圆的短轴长为2.
,椭圆的短轴长为2.
(1)求椭圆的标准方程;
(2)已知直线![]() ,
,![]() 过右焦点
过右焦点![]() ,且它们的斜率乘积为
,且它们的斜率乘积为![]() ,设
,设![]() ,
,![]() 分别与椭圆交于点A,B和C,D.
分别与椭圆交于点A,B和C,D.
①求![]() 的值;
的值;
②设![]() 的中点M,
的中点M,![]() 的中点为N,求
的中点为N,求![]() 面积的最大值.
面积的最大值.
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 经过点
经过点![]() ,其倾斜角为
,其倾斜角为![]() .以原点
.以原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴,与直角坐标系
轴非负半轴为极轴,与直角坐标系![]() 取相同的长度单位,建立极坐标系.设曲线
取相同的长度单位,建立极坐标系.设曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的参数方程,若直线
的参数方程,若直线![]() 与曲线
与曲线![]() 有公共点,求
有公共点,求![]() 的取值范围.
的取值范围.
(2)设![]() 为曲线
为曲线![]() 上任意一点,求
上任意一点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】艾滋病是一种危害性极大的传染病,由感染艾滋病病毒![]() 病毒
病毒![]() 引起,它把人体免疫系统中最重要的CD4T淋巴细胞作为主要攻击目标,使人体丧失免疫功能
引起,它把人体免疫系统中最重要的CD4T淋巴细胞作为主要攻击目标,使人体丧失免疫功能![]() 下表是近八年来我国艾滋病病毒感染人数统计表:
下表是近八年来我国艾滋病病毒感染人数统计表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代码x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
感染者人数 |
|
|
|
|
|
|
| 85 |
![]() 请根据该统计表,画出这八年我国艾滋病病毒感染人数的折线图;
请根据该统计表,画出这八年我国艾滋病病毒感染人数的折线图;

![]() 请用相关系数说明:能用线性回归模型拟合y与x的关系;
请用相关系数说明:能用线性回归模型拟合y与x的关系;
![]() 建立y关于x的回归方程
建立y关于x的回归方程![]() 系数精确到
系数精确到![]() ,预测2019年我国艾滋病病毒感染人数.
,预测2019年我国艾滋病病毒感染人数.
参考数据:![]() ;
;![]() ,
,![]() ,
,![]() ,
,
参考公式:相关系数 ,
,
回归方程![]() 中,
中,![]()
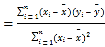 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线方程为
中,抛物线方程为![]() ,其顶点到焦点的距离为
,其顶点到焦点的距离为![]() .
.
(1)求抛物线的方程;
(2)若点![]() ,设直线
,设直线![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 两点,且直线
两点,且直线![]() 、
、![]() 的斜率之和为
的斜率之和为![]() ,试证明:对于任意非零实数
,试证明:对于任意非零实数![]() ,直线
,直线![]() 必过定点.
必过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业对设备进行升级改造,现从设备改造前后生产的大量产品中各抽取了100件产品作为样本,检测一项质量指标值,若该项指标值落在[20,40)内的产品视为合格品,否则为不合格品,图1是设备改造前样本的频率分布直方图,表1是设备改造后的频数分布表.

表1,设备改造后样本的频数分布表:
质量指标值 |
|
|
|
|
|
|
频数 | 2 | 18 | 48 | 14 | 16 | 2 |
(1)请估计该企业在设备改造前的产品质量指标的平均数;
(2)企业将不合格品全部销毁后,并对合格品进行等级细分,质量指标值落在[25,30)内的定为一等品,每件售价240元,质量指标值落在[20,25)或[30,35)内的定为二等品,每件售价180元,其它的合格品定为三等品,每件售价120元.根据表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率,现有一名顾客随机购买两件产品,设其支付的费用为X(单位:元),求X得分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以原点
中,以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.若曲线
轴正半轴为极轴建立极坐标系.若曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]() 点的极坐标为
点的极坐标为![]() ,在平面直角坐标系中,直线
,在平面直角坐标系中,直线![]() 经过点
经过点![]() ,且倾斜角为
,且倾斜角为![]() .
.
(1)写出曲线![]() 的直角坐标方程以及点
的直角坐标方程以及点![]() 的直角坐标;
的直角坐标;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设袋子中装有a个红球,b个黄球,c个蓝球,且规定:取出一个红球得1分,取出一个黄球2分,取出蓝球得3分.
(1)当a=3,b=2,c=1时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量ξ为取出此2球所得分数之和.,求ξ分布列;
(2)从该袋子中任取(且每球取到的机会均等)1个球,记随机变量η为取出此球所得分数.若![]() ,求a:b:c.
,求a:b:c.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com