
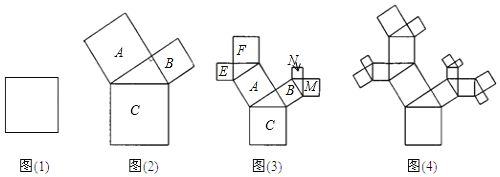
【题目】图一是美丽的“勾股树”,它是一个直角三角形分别以它的每一边向外作正方形而得到.图二是第1代“勾股树”,重复图二的作法,得到图三为第2代“勾股树”,以此类推,已知最大的正方形面积为1,则第![]() 代“勾股树”所有正方形的个数与面积的和分别为( )
代“勾股树”所有正方形的个数与面积的和分别为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
第1代“勾股树”中,小正方形的个数3=21+1﹣1=3,所有正方形的面积之和为2=(1+1)×1,第2代“勾股树”中,小正方形的个数7=22+1﹣1,所有的正方形的面积之和为3=(2+1)×1,以此类推,第n代“勾股树”所有正方形的个数为2n+1﹣1,第n代“勾股树”所有正方形的面积的和为:(n+1)×1=n+1.
解:第1代“勾股树”中,小正方形的个数3=21+1﹣1=3,
如图(2),设直角三角形的三条边长分别为a,b,c,
根据勾股定理得a2+b2=c2,
即正方形A的面积+正方形B的面积=正方形C的面积=1,
所有正方形的面积之和为2=(1+1)×1,
第2代“勾股树”中,小正方形的个数7=22+1﹣1,
如图(3),正方形E的面积+正方形F的面积=正方形A的面积,
正方形M的面积+正方形N的面积=正方形B的面积,
正方形E的面积+正方形F的面积+正方形M的面积+正方形N的面积=正方形A的面积+正方形B的面积=正方形C的面积=1,
所有的正方形的面积之和为3=(2+1)×1,
…
以此类推,第n代“勾股树”所有正方形的个数为2n+1﹣1,
第n代“勾股树”所有正方形的面积的和为:(n+1)×1=n+1.
故选:A.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】2018年2月25日,平昌冬奥会闭幕式上的“北京8分钟”惊艳了世界。我们学校为了让我们更好的了解奥运,了解新时代祖国的科技发展,在高二年级举办了一次知识问答比赛。比赛共设三关,第一、二关各有两个问题,两个问题全答对,可进入下一关;第三关有三个问题,只要答对其中两个问题,则闯关成功。每过一关可一次性获得分别为1、2、3分的积分奖励,高二、一班对三关中每个问题回答正确的概率依次为![]() ,且每个问题回答正确与否相互独立.
,且每个问题回答正确与否相互独立.
(1)记![]() 表示事件“高二、一班未闯到第三关”,求
表示事件“高二、一班未闯到第三关”,求![]() 的值;
的值;
(2)记![]() 表示高二、一班所获得的积分总数,求
表示高二、一班所获得的积分总数,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)请用“五点法”画出函数![]() 在一个周期上的图象(先在所给的表格中填上所需的数字,再画图);
在一个周期上的图象(先在所给的表格中填上所需的数字,再画图);

(2)求![]() 的单调递增区间;
的单调递增区间;
(3)求![]() 在区间
在区间![]() 上的最大值和最小值及相应的
上的最大值和最小值及相应的![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为r米,高为h米,体积为V立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为12000π元(π为圆周率).
(1)将V表示成r的函数V(r),并求该函数的定义域;
(2)讨论函数V(r)的单调性,并确定r和h为何值时该蓄水池的体积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 为椭圆
为椭圆![]() 的左顶点,点
的左顶点,点![]() 为椭圆
为椭圆![]() 的上顶点,且
的上顶点,且![]() .
.
(Ⅰ)若椭圆![]() 的离心率为
的离心率为![]() ,求椭圆
,求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 为椭圆
为椭圆![]() 上一点,且在第一象限内,直线
上一点,且在第一象限内,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,若以
,若以![]() 为直径的圆经过点
为直径的圆经过点![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,梯形ABCD中,AD∥BC,AD=AB=1,AD⊥AB,∠BCD=45°,将△ABD沿对角线BD折起,设折起后点A的位置为A′,使二面角A′—BD—C为直二面角,给出下面四个命题:①A′D⊥BC;②三棱锥A′—BCD的体积为![]() ;③CD⊥平面A′BD;④平面A′BC⊥平面A′DC.其中正确命题的个数是( )
;③CD⊥平面A′BD;④平面A′BC⊥平面A′DC.其中正确命题的个数是( )

A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司要在一条笔直的道路边安装路灯,要求灯柱![]() 与地面垂直,灯杆
与地面垂直,灯杆![]() 与灯柱
与灯柱![]() 所在的平面与道路走向垂直,路灯
所在的平面与道路走向垂直,路灯![]() 采用锥形灯罩,射出的光线与平面
采用锥形灯罩,射出的光线与平面![]() 的部分截面如图中阴影部分所示.已知
的部分截面如图中阴影部分所示.已知![]() ,
,![]() ,路宽
,路宽![]() 米.设
米.设![]()
![]() .
.

(1)求灯柱![]() 的高
的高![]() (用
(用![]() 表示);
表示);
(2)此公司应该如何设置![]() 的值才能使制造路灯灯柱
的值才能使制造路灯灯柱![]() 与灯杆
与灯杆![]() 所用材料的总长度最小?最小值为多少?
所用材料的总长度最小?最小值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() ,底面
,底面![]() 为菱形,
为菱形, ![]() ,H为
,H为![]() 上的点,过
上的点,过![]() 的平面分别交
的平面分别交![]() 于点
于点![]() ,且
,且![]() 平面
平面![]() .
.

(1)证明: ![]() ;
;
(2)当![]() 为
为![]() 的中点,
的中点, ![]() ,
,![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现要完成下列三项抽样调查:①从![]() 罐奶粉中抽取
罐奶粉中抽取![]() 罐进行食品安全卫生检查;②高二年级有
罐进行食品安全卫生检查;②高二年级有![]() 名学生,为调查学生的学习情况抽取一个容量为
名学生,为调查学生的学习情况抽取一个容量为![]() 的样本;③从某社区
的样本;③从某社区![]() 户高收入家庭,
户高收入家庭,![]() 户中等收入家庭,
户中等收入家庭,![]() 户低收入家庭中选出
户低收入家庭中选出![]() 户进行消费水平调查.以下各调查方法较为合理的是( )
户进行消费水平调查.以下各调查方法较为合理的是( )
A.①系统抽样,②简单随机抽样,③分层抽样
B.①简单随机抽样,②分层抽样,③系统抽样
C.①分层抽样,②系统抽样,③简单随机抽样
D.①简单随机抽样,②系统抽样,③分层抽样
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com