
求同时满足下列条件的所有复数z:(1)![]() 是实数,且
是实数,且![]() 。
。
(2)z的实部和虚部都是整数。
科目:高中数学 来源:2010年江苏省启东中学高二下学期期中考试数学(理) 题型:解答题
(16分)求同时满足下列条件的w*w^w.k&s#5@u.c~o*m所有的复数z,
①z+ ∈R, 且1<z+
∈R, 且1<z+ ≤6;②z的实部和虚部都是整数.[来源:Z&xx&k.Com]
≤6;②z的实部和虚部都是整数.[来源:Z&xx&k.Com]
查看答案和解析>>
科目:高中数学 来源:2010年江苏省高二下学期期中考试数学(理) 题型:解答题
(16分)求同时满足下列条件的所有的复数z,
①z+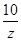 ∈R, 且1<z+
∈R, 且1<z+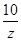 ≤6;②z的实部和虚部都是整数.[来源:Z&xx&k.Com]
≤6;②z的实部和虚部都是整数.[来源:Z&xx&k.Com]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com