
| 家庭类型 | 贫困 | 温饱 | 小康 | 富裕 |
| n | n≥59% | 50%≤n<59% | 40%≤n<50% | 30%≤n<40% |
分析 首先设出2000年人均食品消费,然后分别表示出2004年人均食品支出、2004年人均消费支出.最后根据题意列出等式,求出未知数即可.
解答 解:设2000年人均食品消费x元,
则2004年人均食品支出:x(1-7.5%)=92.5%x,
2004年人均消费支出:2×92.5%x+475,
由题意,有:2×92.5%x+475+75=2x+475,解得:x=500,
此时,x=$\frac{92.5%x}{2×92.5%x+475}$=$\frac{462.5}{1400}$≈0.3304=33.04%,
于是该家庭2004年生活水平状况为富裕.
点评 本题考查函数模型的选择与应用,考查运算求解能力,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>c>a | C. | c>b>a | D. | a>c>b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在底面为平行四边形的四棱柱ABCD-A1B1C1D1中,设M是上底面A1B1C1D1的中心.
如图所示,在底面为平行四边形的四棱柱ABCD-A1B1C1D1中,设M是上底面A1B1C1D1的中心.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
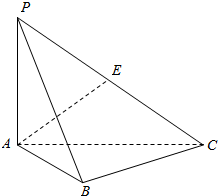 己知三棱锥P-ABC,PA⊥底面ABC,PA=AB=BC=2,直线PC与平面ABC所成的角为arctan$\frac{\sqrt{2}}{2}$.
己知三棱锥P-ABC,PA⊥底面ABC,PA=AB=BC=2,直线PC与平面ABC所成的角为arctan$\frac{\sqrt{2}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com