
【题目】某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生的样本数据?
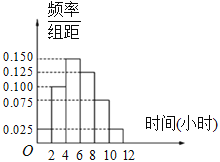
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为:![]() ,试估计该校学生每周平均体育运动时间超过4小时的概率.
,试估计该校学生每周平均体育运动时间超过4小时的概率.
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4小时.请完成每周平均体育运动时间与性别的列联表,并判断能否在犯错误的概率不超过0.05的前提下认为该校学生的每周平均体育运动时间与性别有关?
男生 | 女生 | 合计 | |
每周平均体育运动时间不超过4小时 | |||
每周平均体育运动时间超过4小时 | |||
合计 | 300 |
附:![]() ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【答案】见解析
【解析】(1)由![]() ,得应收集90位女生的样本数据.(3分)
,得应收集90位女生的样本数据.(3分)
(2)由频率分布直方图得每周平均体育运动时间超过4小时的频率为![]() ,由频率估计概率得该校学生每周平均体育运动时间超过4小时的概率为0.75. (7分)
,由频率估计概率得该校学生每周平均体育运动时间超过4小时的概率为0.75. (7分)
(3)由(2)知,300位学生中有300×0.75=225人的每周平均体育运动时间超过4小时,75人每周平均体育运动时间不超过4小时,又因为样本数据中有210份是关于男生的,90份是关于女生的,所以每周平均体育运动时间与性别的列联表如下:
男生 | 女生 | 合计 | |
每周平均体育运动时间不超过4小时 | 45 | 30 | 75 |
每周平均体育运动时间超过4小时 | 165 | 60 | 225 |
合计 | 210 | 90 | 300 |
(10分)
因为![]() 的观测值
的观测值![]() ,
,
所以能在犯错误的概率不超过0.05的前提下认为该校学生的每周平均体育运动时间与性别有关.(12分)


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】已知m>1,直线l:x﹣my﹣ ![]() =0,椭圆C:
=0,椭圆C: ![]() +y2=1,F1、F2分别为椭圆C的左、右焦点. (Ⅰ)当直线l过右焦点F2时,求直线l的方程;
+y2=1,F1、F2分别为椭圆C的左、右焦点. (Ⅰ)当直线l过右焦点F2时,求直线l的方程;
(Ⅱ)设直线l与椭圆C交于A、B两点,△AF1F2 , △BF1F2的重心分别为G、H.若原点O在以线段GH为直径的圆内,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=loga(3﹣ax)(a>0,a≠1)
(1)当a=2时,求函数f(x)的定义域;
(2)是否存在实数a,使函数f(x)在[1,2]递减,并且最大值为1,若存在,求出a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2x,x∈(4,8),则函数y=f(x2)+ ![]() 的值域为( )
的值域为( )
A.[8,10)
B.( ![]() ,10)
,10)
C.(8, ![]() )
)
D.( ![]() ,10)
,10)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现在的安卓手机盛行一款“心有灵犀”的猜数字游戏,具体的规则如下:
玩家随机输入0~5中的三位数字(数字不重复),按“OK”键确定答案是否正确,手机会给出“xAyB”的提示,其中“xA”表示你输入的三位数字中,有“x”个数字和位置都与答案相同,其中“yB”表示你输入的三位数字中,有“y”个数字与答案相同,但是位置不同,例如:答案为“012”,当你输入“132”时会显示:“1A1B”.
(1)当你第一次输入时,手机显示“1A1B”的概率为多少?
(2)当你第一次输入时,且手机显示“xA2B”时,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题P:方程x2+mx+1=0有两个不等的实数根,命题q:方程4x2+4(m﹣2)x+1=0无实数根.若p∧q为假,若p∨q为真,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
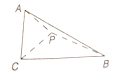
【题目】已知直角三角形![]() 的两条直角边
的两条直角边![]() ,
, ![]() ,
, ![]() 为斜边
为斜边![]() 上一点,沿
上一点,沿![]() 将三角形折成直二面角
将三角形折成直二面角![]() ,此时二面角
,此时二面角![]() 的正切值为
的正切值为![]() ,则翻折后
,则翻折后![]() 的长为( )
的长为( )
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两条不重合的直线![]() 和两个不重合的平面
和两个不重合的平面![]() ,若
,若![]() ,则下列四个命题:①若
,则下列四个命题:①若![]() ,则
,则![]() ;②若
;②若![]() ,则
,则![]() ; ③若
; ③若![]() ,则
,则![]() ;④若
;④若![]() ,则
,则![]() ,其中正确命题的个数是( )
,其中正确命题的个数是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com