
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,侧棱
,侧棱![]() 面
面![]() ,
,![]() .
.
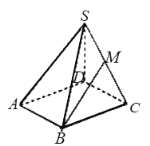
(1)若![]() 是
是![]() 的中点,求
的中点,求![]() 与
与![]() 所成的角;
所成的角;
(2)设![]() 是
是![]() 上一点,过
上一点,过![]() 的平面将四棱柱
的平面将四棱柱![]() 分成体积相等的两部分,求
分成体积相等的两部分,求![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)设菱形![]() 的边长为单位1,则
的边长为单位1,则![]() .取
.取![]() 的中点
的中点![]() ,连接
,连接![]() .可得
.可得![]() (或其补角)就是
(或其补角)就是![]() 与
与![]() 所成的角.在
所成的角.在![]() 中求出这个角即可;
中求出这个角即可;
(2)作出过![]() 的平面与侧面
的平面与侧面![]() 的交线为
的交线为![]() .可证得
.可证得![]() ,设
,设![]() ,
,![]() ,多面体
,多面体![]() 的体积等于三棱锥
的体积等于三棱锥![]() 与四棱锥
与四棱锥![]() 的体积之和,由此求得
的体积之和,由此求得![]() ,可得
,可得![]() .
.
设菱形![]() 的边长为单位1,则
的边长为单位1,则![]() .
.
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
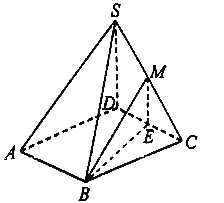
∵![]() 是
是![]() 是中点,∴
是中点,∴![]() ,
,![]() ,
,![]() ,
,![]() (或其补角)就是
(或其补角)就是![]() 与
与![]() 所成的角.
所成的角.
∵![]() 面
面![]() ,∴
,∴![]() 面
面![]() ,而
,而![]() 面
面![]() ,∴
,∴![]() .
.
在![]() 中,因为
中,因为![]() ,
,![]() ,
,
所以![]() ,即
,即![]() .
.
从而在![]() 中,
中,![]() ,故
,故![]() .
.
∴异面直线![]() 与
与![]() 所成的角的60°.
所成的角的60°.
(2)如图,设过![]() 的平面与侧面
的平面与侧面![]() 的交线为
的交线为![]() .
.
∵![]() ,
,![]() 不在平面
不在平面![]() 内,∴
内,∴![]() 面
面![]() ,∴
,∴![]() ,于是
,于是![]() .
.
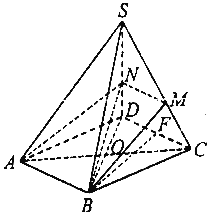
连接![]() ,
,![]() ,
,![]() ,设
,设![]() ,
,![]() ,
,
则直角梯形![]() 中,
中,![]() ,其面积
,其面积![]() .
.
过![]() 在平面
在平面![]() 内作
内作![]() ,
,![]() 是垂足,在等边三角形
是垂足,在等边三角形![]() 中,
中,![]() .
.
∵![]() 面
面![]() ,∴
,∴![]() ,得
,得![]() 面
面![]() ,
,
多面体![]() 的体积
的体积![]()
![]()
![]() ,
,
∴![]() ,
,![]() (舍去大于1的).
(舍去大于1的).
由![]() ,得
,得![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 是自然对数的底数)
是自然对数的底数)
(1)若直线![]() 为曲线
为曲线![]() 的一条切线,求实数
的一条切线,求实数![]() 的值;
的值;
(2)若函数![]() 在区间
在区间![]() 上为单调函数,求实数
上为单调函数,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,若
,若![]() 在定义域上有极值点(极值点是指函数取得极值时对应的自变量的值),求实数
在定义域上有极值点(极值点是指函数取得极值时对应的自变量的值),求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在明代程大位所著的《算法统宗》中有这样一首歌谣,“放牧人粗心大意,三畜偷偷吃苗青,苗主扣住牛马羊,要求赔偿五斗粮,三畜户主愿赔偿,牛马羊吃得异样.马吃了牛的一半,羊吃了马的一半.”请问各畜赔多少?它的大意是放牧人放牧时粗心大意,牛、马、羊偷吃青苗,青苗主人扣住牛、马、羊向其主人要求赔偿五斗粮食(1斗=10升),三畜的主人同意赔偿,但牛、马、羊吃的青苗量各不相同.马吃的青苗是牛的一半,羊吃的青苗是马的一半.问羊、马、牛的主人应该分别向青苗主人赔偿多少升粮食?( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() 在点
在点![]() 处的切线斜率为0.
处的切线斜率为0.
(1)试用含有![]() 的式子表示
的式子表示![]() ,并讨论
,并讨论![]() 的单调性;
的单调性;
(2)对于函数![]() 图象上的不同两点
图象上的不同两点![]() ,
,![]() ,如果在函数
,如果在函数![]() 图象上存在点
图象上存在点![]() ,使得在点
,使得在点![]() 处的切线
处的切线![]() ,则称
,则称![]() 存在“跟随切线”.特别地,当
存在“跟随切线”.特别地,当![]() 时,又称
时,又称![]() 存在“中值跟随切线”.试问:函数
存在“中值跟随切线”.试问:函数![]() 上是否存在两点
上是否存在两点![]() 使得它存在“中值跟随切线”,若存在,求出
使得它存在“中值跟随切线”,若存在,求出![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产的某种产品,如果年返修率不超过千分之一,则其生产部门当年考核优秀,现获得该公司2011-2018年的相关数据如下表所示:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年生产台数(万台) | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 11 |
该产品的年利润(百万元) | 2.1 | 2.75 | 3.5 | 3.25 | 3 | 4.9 | 6 | 6.5 |
年返修台数(台) | 21 | 22 | 28 | 65 | 80 | 65 | 84 | 88 |
部分计算结果:
| ||||||||
注:年返修率=![]()
(1)从该公司2011-2018年的相关数据中任意选取3年的数据,以![]() 表示3年中生产部门获得考核优秀的次数,求
表示3年中生产部门获得考核优秀的次数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)根据散点图发现2015年数据偏差较大,如果去掉该年的数据,试用剩下的数据求出年利润![]() (百万元)关于年生产台数
(百万元)关于年生产台数![]() (万台)的线性回归方程(精确到0.01).
(万台)的线性回归方程(精确到0.01).
附:线性回归方程![]() 中,
中,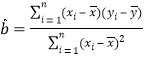
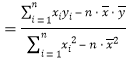 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
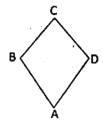
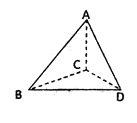
【题目】等腰直角三角形BCD与等边三角形ABD中,![]() ,
,![]() ,现将
,现将![]() 沿BD折起,则当直线AD与平面BCD所成角为
沿BD折起,则当直线AD与平面BCD所成角为![]() 时,直线AC与平面ABD所成角的正弦值为( )
时,直线AC与平面ABD所成角的正弦值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,过
,过![]() ,
,![]() 分别作
分别作![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() ,
,![]() ,已知
,已知![]() ,
,![]() ,将梯形
,将梯形![]() 沿
沿![]() ,
,![]() 同侧折起,使得平面
同侧折起,使得平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,得到图2.
,得到图2.
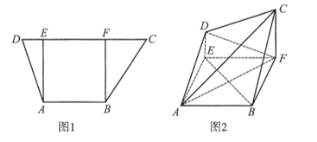
(1)证明:![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
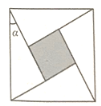
【题目】在古代三国时期吴国的数学家赵爽创制了一幅“赵爽弦图”,由四个全等的直角三角形围成一个大正方形,中间空出一个小正方形(如图阴影部分)。若直角三角形中较小的锐角为a。现向大正方形区城内随机投掷一枚飞镖,要使飞镖落在小正方形内的概率为![]() ,则
,则![]() _____________。
_____________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com