
分析 (1)联立方程得出l1,l3交于A(-1,0),l2,l3交于B(0,m+1)从而可以证明结论.
(2)首先根据条件得出角C为直角,从而得出S=$\frac{1}{2}$|AC|•|BC|,再利用点到直线的距离公式得出BC,AC,然后利用均值不等式求出,$\frac{1}{m+\frac{1}{m}}$的最值,即可得出结果.
解答 (1)证明:根据题意得 l1,l3交于A(-1,0)l2,l3交于B(0,m+1)
∴不论m取何值时,△ABC中总有一个顶点为定点(-1,0)
(2)解:从条件中可以看出l1、l2垂直
∴角C为直角,
∴S=$\frac{1}{2}$|AC|•|BC|
|BC|等于点(0,m+1)到l1的距离d=$\frac{|-m-1+m|}{\sqrt{{m}^{2}+1}}$=$\frac{1}{\sqrt{{m}^{2}+1}}$
|AC|等于(-1,0)到l2的距离d=$\frac{{m}^{2}+m+1}{\sqrt{{m}^{2}+1}}$
S=$\frac{1}{2}$×$\frac{{m}^{2}+m+1}{\sqrt{{m}^{2}+1}}$=$\frac{1}{2}$[1+$\frac{1}{m+\frac{1}{m}}$]
当m>0时,$\frac{1}{m+\frac{1}{m}}$有最大值$\frac{1}{2}$
同理,当m<0时,$\frac{1}{m+\frac{1}{m}}$有最小-$\frac{1}{2}$
∴m=1时S取最大值为$\frac{3}{4}$,m=-1时S取最小值$\frac{1}{4}$.
点评 本题考查了两条直线的交点坐标以及基本不等式的最值问题,此题有一定难度,属于中档题.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:解答题
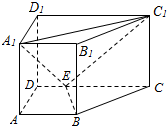 如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD=$\sqrt{2}$,AA1=3,E为CD上一点,DE=1,EC=3.
如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD=$\sqrt{2}$,AA1=3,E为CD上一点,DE=1,EC=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
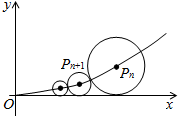 在xOy平面上有一系列点P1(x1,y1),P2(x2,y2),…Pn(xn,yn)对每个正整数n,点Pn位于函数y=x2(x≥0)的图象上,以点Pn为圆心的圆Pn与H轴都相切,且圆Pn与圆Pn+1又彼此外切.若x1=1,且xn+1<xn(n∈N+).
在xOy平面上有一系列点P1(x1,y1),P2(x2,y2),…Pn(xn,yn)对每个正整数n,点Pn位于函数y=x2(x≥0)的图象上,以点Pn为圆心的圆Pn与H轴都相切,且圆Pn与圆Pn+1又彼此外切.若x1=1,且xn+1<xn(n∈N+).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(-1)<f(1)<f(4) | B. | f(1)<f(-1)<f(4) | C. | f(-1)<f(4)<f(1) | D. | f(4)<f(-1)<f(1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|3≤x≤4} | B. | {x|3<x≤4} | C. | {x|x=2或3<x≤4} | D. | {x|3<x<4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2014,+∞) | B. | (-∞,0)∪(2014,+∞) | C. | (-∞,0)∪(0,+∞) | D. | (-∞,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com