【题目】某车间租赁甲、乙两种设备生产A，B两类产品，甲种设备每天能生产A类产品8件和B类产品15件，乙种设备每天能生产A类产品10件和B类产品25件，已知设备甲每天的租赁费300元，设备乙每天的租赁费400元，现车间至少要生产A类产品100件，B类产品200件，所需租赁费最少为__元
期末宝典单元检测分类复习卷系列答案科目：高中数学 来源： 题型：
【题目】求解下列各题.
(1)已知
,且
为第一象限角,求
,
;
(2)已知
,且为第三象限角,求
,;
(3)已知
,且为第四象限角,求,;
(4)已知
,且为第二象限角,求,.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某高三理科班共有60名同学参加某次考试，从中随机挑选出5名同学，他们的数学成绩
与物理成绩
如下表：
数据表明与之间有较强的线性关系.
（1）求关于的线性回归方程；
（2）该班一名同学的数学成绩为110分，利用（1）中的回归方程，估计该同学的物理成绩；
（3）本次考试中，规定数学成绩达到125分为优秀，物理成绩达到100分为优秀.若该班数学优秀率与物理优秀率分别为
和
，且除去抽走的5名同学外，剩下的同学中数学优秀但物理不优秀的同学共有5人.能否在犯错误概率不超过0.01的前提下认为数学优秀与物理优秀有关？
参考数据:回归直线的系数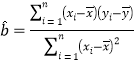
，
.
，
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，已知圆
的方程为：
，直线
的方程为
.
（1）求证：直线恒过定点；
（2）当直线被圆截得的弦长最短时，求直线的方程；
（3）在（2）的前提下，若
为直线上的动点，且圆上存在两个不同的点到点的距离为
，求点的横坐标的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥
中，底面
为直角梯形， 
， 
，平面
底面
， 
为
的中点， 
， 
是棱
上的点.
（1）求证：平面
平面
；
（2）若
， 
， 
，异面直线
与
所成角的余弦值为
，求
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，
的直角边OA在x轴上，顶点B的坐标为
，直线CD交AB于点
，交x轴于点
.
(1)求直线CD的方程；
(2)动点P在x轴上从点
出发，以每秒1个单位的速度向x轴正方向运动，过点P作直线l垂直于x轴，设运动时间为t.
①点P在运动过程中，是否存在某个位置，使得
?若存在，请求出点P的坐标；若不存在，请说明理由；
②请探索当t为何值时，在直线l上存在点M，在直线CD上存在点Q，使得以OB为一边，O，B，M，Q为顶点的四边形为菱形，并求出此时t的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标中xOy，圆C1：x2+y2=8，圆C2：x2+y2=18，点M（1，0），动点A、B分别在圆C1和圆C2上，满足
，则
的取值范围是______．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在平面直角坐标系
中，椭圆： 
的离心率为
，直线l：y＝2上的点和椭圆上的点的距离的最小值为1．
(Ⅰ) 求椭圆的方程；
(Ⅱ) 已知椭圆的上顶点为A，点B，C是上的不同于A的两点，且点B，C关于原点对称，直线AB，AC分别交直线l于点E，F．记直线
与
的斜率分别为
， 
．
① 求证： 
为定值；
② 求△CEF的面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
