
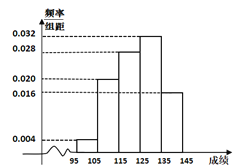
【题目】半期考试后,班长小王统计了50名同学的数学成绩,绘制频率分布直方图如图所示.
![]() 根据频率分布直方图,估计这50名同学的数学平均成绩;
根据频率分布直方图,估计这50名同学的数学平均成绩;
![]() 用分层抽样的方法从成绩低于115的同学中抽取6名,再在抽取的这6名同学中任选2名,求这两名同学数学成绩均在
用分层抽样的方法从成绩低于115的同学中抽取6名,再在抽取的这6名同学中任选2名,求这两名同学数学成绩均在![]() 中的概率.
中的概率.
【答案】(1)![]() (2)
(2)![]()
【解析】
⑴用频率分布直方图中的每一组数据的平均数乘以对应的概率并求和即可得出结果;
⑵首先可通过分层抽样确定6人中在![]() 分数段以及
分数段以及![]() 分数段中的人数,然后分别写出所有的基本事件以及满足题意中“两名同学数学成绩均在
分数段中的人数,然后分别写出所有的基本事件以及满足题意中“两名同学数学成绩均在![]() 中”的基本事件,最后两者相除,即可得出结果。
中”的基本事件,最后两者相除,即可得出结果。
⑴由频率分布表,估计这50名同学的数学平均成绩为:
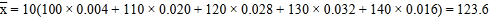 ;
;
⑵由频率分布直方图可知分数低于115分的同学有![]() 人,
人,
则用分层抽样抽取6人中,分数在![]() 有1人,用a表示,
有1人,用a表示,
分数在![]() 中的有5人,用
中的有5人,用![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 表示,
表示,
则基本事件有![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、
![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共15个,
,共15个,
满足条件的基本事件为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共10个,
,共10个,
所以这两名同学分数均在![]() 中的概率为
中的概率为![]() 。
。


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,记
,记![]() 为与原点距离等于
为与原点距离等于![]() 的全体直线所成的集合.问:是否存在常数
的全体直线所成的集合.问:是否存在常数![]() ,使得对任意的直线
,使得对任意的直线![]() ,均存在
,均存在![]() 、
、![]() ,
,![]() 、
、![]() 分别过
分别过![]() 与椭圆
与椭圆![]() 的交点
的交点![]() 、
、![]() ,且有
,且有![]() ?并说明理由.
?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以坐标原点为中心,以坐标轴为对称轴的椭圆C经过点M(2,1),N(![]() ,-
,-![]() ).
).
(1)求椭圆C的标准方程;
(2)经过点M作倾斜角互补的两条直线,分别与椭圆C相交于异于M点的A,B两点,求直线AB的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() :
:![]() ,过抛物线焦点
,过抛物线焦点![]() 且与
且与![]() 轴垂直的直线与抛物线相交于
轴垂直的直线与抛物线相交于![]() 、
、![]() 两点,且
两点,且![]() 的周长为
的周长为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若直线![]() 过焦点
过焦点![]() 且与抛物线
且与抛物线![]() 相交于
相交于![]() 、
、![]() 两点,过点
两点,过点![]() 、
、![]() 分别作抛物线
分别作抛物线![]() 的切线
的切线![]() 、
、![]() ,切线
,切线![]() 与
与![]() 相交于点
相交于点![]() ,求:
,求:![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子科技公司由于产品采用最新技术,销售额不断增长,最近![]() 个季度的销售额数据统计如下表(其中
个季度的销售额数据统计如下表(其中![]() 表示
表示![]() 年第一季度,以此类推):
年第一季度,以此类推):
季度 |
|
|
|
|
|
季度编号x |
|
|
|
|
|
销售额y(百万元) |
|
|
|
|
|
(1)公司市场部从中任选![]() 个季度的数据进行对比分析,求这
个季度的数据进行对比分析,求这![]() 个季度的销售额都超过
个季度的销售额都超过![]() 千万元的概率;
千万元的概率;
(2)求![]() 关于
关于![]() 的线性回归方程,并预测该公司
的线性回归方程,并预测该公司![]() 的销售额.
的销售额.
附:线性回归方程:![]() 其中
其中 ,
,![]()
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小型企业甲产品生产的投入成本x(单位:万元)与产品销售收入y(单位:万元)存在较好的线性关系,下表记录了最近5次该产品的相关数据.
x(万元) | 3 | 5 | 7 | 9 | 11 |
y(万元) | 8 | 10 | 13 | 17 | 22 |
(1)求y关于x的线性回归方程;
(2)根据(1)中的回归方程,判断该企业甲产品投入成本12万元的毛利率更大还是投入成本15万元的毛利率更大(毛利率![]()
![]()
![]() )?
)?
相关公式: ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com