【题目】已知各项都为正数的数列{an}满足a1＝1， 
＝2an＋1(an＋1)－an.
(Ⅰ)求数列{an}的通项公式；
(Ⅱ)设bn＝
，求数列{an·bn}的前n项和Tn.
【答案】(Ⅰ)an＝(
)n－1(Ⅱ)Tn＝2－(n＋1)( 
)n－1.
【解析】试题分析：(Ⅰ)由
＝2an＋1(an＋1)－an，化简可得
.进而可得an＝(
)n－1.
(Ⅱ) 根据错位相减法，即可求出数列的数列{an·bn}的前n项和Tn.
试题解析：(Ⅰ)由
＝2an＋1(an＋1)－an，
得2an＋1(an＋1)＝an(an＋1)，
因为数列{an}的各项都为正数，所以
.
故数列{an}是首项为1，公比为
的等比数列，因此an＝(
)n－1.
(Ⅱ)由(Ⅰ)知an＝(
)n－1，故bn＝n－1，所以an·bn＝(n－1)( 
)n－1，数列{an·bn}的前n项和Tn＝
＋2×(
)2＋3×(
)3＋…＋(n－2)×(
)n－2＋(n－1)×(
)n－1①
Tn＝(
)2＋2×(
)3＋3×(
)4＋…＋(n－2)×(
)n－1＋(n－1)×(
)n，②
①－②得
Tn＝
＋(
)2＋(
)3＋…＋(
)n－1－(n－1)×(
)n
＝
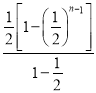－(n－1)×(
)n＝1－(
)n－1－(n－1)×(
)n＝1－(n＋1)( 
)n，
Tn＝2－(n＋1)( 
)n－1.
能力评价系列答案
唐印文化课时测评系列答案科目：高中数学 来源： 题型：
【题目】在直角坐标系xOy中，直线l的参数方程为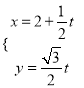
(t为参数)，若以该直角坐标系的原点O为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρsin2θ－4cos θ＝0.
(1)求直线l与曲线C的普通方程；
(2)已知直线l与曲线C交于A，B两点，设M(2，0)，求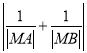
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】
近年来，随着双十一、双十二等网络活动的风靡，各大网商都想出了一系列的降价方案，以此来提高自己的产品利润. 已知在2016年双十一某网商的活动中，某店家采取了两种优惠方案以供选择：
方案一：购物满400元以上的，超出400元的部分只需支出超出部分的x%；
方案二：购物满400元以上的，可以参加电子抽奖活动，即从1,2,3,4,5,6这6张卡牌中任取2张，将得到的数字相加，所得结果与享受优惠如下：
数字和 | [3,4] | [5,7] | [8,9] | [10,11] |
实际付款 | 原价 | 9折 | 8折 | 5折 |
(Ⅰ)若某顾客消费了800元，且选择方案二，求该顾客只需支付640元的概率；
(Ⅱ)若某顾客购物金额为500元，她选择了方案二后，得到的数字之和为6，此时她发现使用方案一、二最后支付的金额相同，求x的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】以平面直角坐标系的原点为极点，x轴正半轴为极轴建立极坐标系．已知圆C的极坐标方程为ρ＝2sin θ，直线l的参数方程为
(t为参数)，若l与C交于A，B两点．
(Ⅰ)求|AB|；
(Ⅱ)设P(1,2)，求|PA|·|PB|的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)＝x2－aln x(a>0)的最小值是1.
(1)求a；
(2)若关于x的方程f2(x)ex－6mf(x)＋9me－x＝0在区间[1，＋∞)有唯一的实根，求m的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】高三一班、二班各有6名学生去参加学校组织的高中数学竞赛选拔考试，成绩如茎叶图所示.
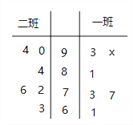
（1）若一班、二班6名学生的平均分相同，求
值；
（2）若将竞赛成绩在
、
、
内的学生在学校推优时，分别赋分、2分、3分，现在从一班的6名参赛学生中选两名，求推优时，这两名学生赋分的和为4分的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】(导学号：05856262)
如图所示，在斜三棱柱ABC－A1B1C1中，AB＝BC＝1，AA1＝2，D是AC的中点，AB⊥平面B1C1CB，∠BCC1＝60°.
(Ⅰ)求证：AC⊥平面BDC1；
(Ⅱ)E是线段CC1上的动点，判断点E到平面AA1B1B的距离是否为定值，若是，求出此定值；否则，说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
