
分析 (1)由两角和的正弦公式、二倍角余弦公式变形化简解析式,由余弦函数的性质和整体思想,求出f(x)的最小正周期及单调增区间;
(2)由x的范围求出“2x”的范围,由正弦函数的性质,求出f(x)在区间$[{-\frac{π}{4},\frac{3π}{8}}]$上的最值.
解答 解:(1)$f(x)=1-2si{n}^{2}(x+\frac{π}{8})+2sin(x+\frac{π}{8})cos(x+\frac{π}{8})$
=$1-[1-cos(2x+\frac{π}{4})]+sin(2x+\frac{π}{4})$
=$cos(2x+\frac{π}{4})+sin(2x+\frac{π}{4})$=$\sqrt{2}sin(2x+\frac{π}{4}+\frac{π}{4})$
=$\sqrt{2}cos2x$
所以f(x)的最小正周期T=$\frac{2π}{2}=π$,
由-π+2kπ≤2x≤2kπ(k∈z)得,$-\frac{π}{2}+kπ≤x≤kπ(k∈z)$,
所以f(x)的单调增区间是$[-\frac{π}{2}+kπ,kπ](k∈z)$;
(2)由$x∈[-\frac{π}{4},\frac{3π}{8}]$得,$2x∈[-\frac{π}{2},\frac{3π}{4}]$,
则$cos2x∈[-\frac{\sqrt{2}}{2},1]$,即$f(x)=\sqrt{2}cos2x∈[-1,\sqrt{2}]$,
所以f(x)在区间$[{-\frac{π}{4},\frac{3π}{8}}]$上的最大值是$\sqrt{2}$、最小值是-1.
点评 本题考查正弦函数的性质,两角和的正弦公式、二倍角余弦公式变形等,及三角形的周期公式的应用,考查整体思想,化简、变形能力.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:选择题
| A. | 若a⊥b,a⊥α,b?α,则b∥α | B. | 若a⊥b,a⊥α,b⊥β,则α⊥β | ||
| C. | 若a⊥β,α⊥β,则a∥α或a?α | D. | 若a∥α,α⊥β,则a⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 数列{bn}是等差数列,{bn}的公差也为d | |
| B. | 数列{bn}是等差数列,{bn}的公差为2d | |
| C. | 数列{an+bn}是等差数列,{an+bn}的公差为d | |
| D. | 数列{an-bn}是等差数列,{an-bn}的公差为$\frac{d}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
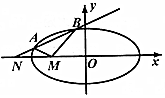 已知椭圆C:$\frac{{x}^{2}}{2}$$+\frac{{y}^{2}}{n}$=1(0<n<2).
已知椭圆C:$\frac{{x}^{2}}{2}$$+\frac{{y}^{2}}{n}$=1(0<n<2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com